Такая модель описывает, например, статическое воздействие на состояние ЭО управляющих финансовых факторов Ck,t , полученных из различных источников (k = 0, 1, 2, …, K), или динамическое воздействие, если Ck,t º Ck-t .
Если все структурные параметры (коэффициенты) динамического уравнения (1.1.2) известны, то при некоторых допущениях о характере поведения помехи Ht возможно определить значение St состояния ЭО в любой момент времени. Следовательно, возможно спланировать финансовые затраты, необходимые для достижения ЭО заданного (планового) значения S*n или «выхода» на плановую траекторию S*n+1, S*n+2, …, S*n+T к определенному моменту времени t = n (см. рис. 1.1.1).
Однако на практике часто бывает так, что известны не коэффициенты уравнения состояния ЭО, а лишь некоторые наблюдения (ряды) данных C1, C2, … , Cn и S1, S2, … , Sn для конкретного процесса. По этим эмпирическим данным необходимо спрогнозировать будущие значения Sn+1, Sn+2, … , Sm состояния ЭО.
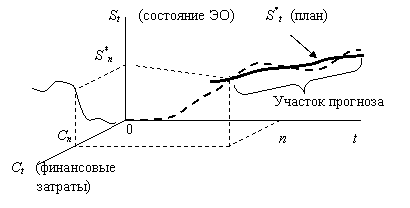 |
РРис. 1.1.1
При этом возникают две проблемы:
- идентификация параметров уравнения (структурная идентификация ЭО) по этим эмпирическим данным;
- прогноз будущих значений Sn+1, Sn+2, … , Sm состояния ЭО на основе идентифицированных параметров.
Естественно, что основную роль в обоих случаях играет как характер помех, так и характер нестационарности параметров соответствующего динамического уравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.