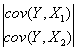Информационные технологии прогнозирования состояний экономических объектов, страница 26

= = / Det_å.          

Следовательно, коэффициенты предиктора и точность предсказания определяются выражениями

b₁ = ,   (2.3.10)

b₂ = ,

b₀ = áYñ – b₁áX₁ñ – b₂áX₂ñ,                                                      

h_YX² = [b₁ cov(Y, X₁) + b₂ cov(Y, X₂)] / s_Y²  .  

Для частного случая статистически независимых (ортогональных) переменных X₁ и X₂ , для которых cov(X₁, X₂) = 0, получим

b₁  =   =  cov(Y, X₁) /s_X1²,                         (2.3.11)

b₂  =  =  cov(Y, X₁) /s_X2²,

b₀ = áYñ – áX₁ñ – áX₂ñ,                 

h_YX² = [+ ] / s_Y²  .  

Синтез нелинейного предиктора

для экспертного оценивания.

Предположим, что ЭО зависит от многомерного вектора структурных параметров (факторов) P = (P₁, P₂, …, P_N). Пусть известны M эталонных состояний ЭО (M < N) с соответствующими векторами  P_m = (P_m1, P_m2, …, P_mN) (m = 1, 2, …, M). Пусть также в каждом эталонном состоянии ЭО известны значения Y_m некоторого параметра Y состояния ЭО. Необходимо синтезировать регрессионную оценку параметра Y ЭО для произвольного значения P.