Информационные технологии прогнозирования состояний экономических объектов, страница 20

y = r_Y(x) = ò y Pr(x, y) dy /ò Pr(x, y) dy .                                   (2.1.7)

Это означает, что ошибка определения статистической связи между  случайными величинами Y и  X отсутствует. Статистическая связь полностью определяется регрессионной зависимостью (2.1.7).

Заметим, что подобно тому, как среднее (математическое ожидание) является важнейшей характеристикой распределения, регрессия является важнейшей характеристикой условного распределения.

Пример 2.1.1. Пусть совместное распределение случайных величин X и Y описывается нормальной плотностью вероятностей с áxñ, áyñ, D(x) = s_X² = áx²ñ, D(y) = s_Y² = áy²ñ, cor(x, y) = r_XY , ½r_XY ½< 1. Тогда

Pr(x, y)=N(áxñ,áyñ;COV_XY), Pr(yú x)=N(r(x);(1-r_XY²)s_Y²), (2.1.8)

где

COV_XY   =   ,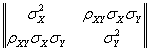

COV^-1_XY =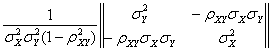 

или

Pr(x, y) = exp{– [(x – áxñ)²/s_X² – 2r_XY (x – áxñ)(y – áyñ)/s_X s_Y +

+ (y – áyñ)²/s_Y²]/2(1 – r_XY²)}/ 2p s_X s_Y (1 – r_XY²)^1/2,

Pr(yú x) = Pr(x, y) / Pr(x) =                                               (2.1.9)