Информационные технологии прогнозирования состояний экономических объектов, страница 24

r(x₁, x₂, … , x_n-1) = áx_nñ – (x_k – áx_kñ) s ^kn /s ⁿⁿ ,                                                                

s_YX²   = 1/s ⁿⁿ, s_R²  = s_nn – 1/s ⁿⁿ,

h_YX²   = 1 – 1/(s_nn s ⁿⁿ).

2.3. Синтез предикторов.

Синтез линейного предиктора.

Пусть предиктор описывается функцией множественной линейной регрессии

Y = b₀ + b₁X₁ + b₂X₂ + … b_pX _p = b₀ + b ⁺ X.               (2.3.1)

В (2.4.1) введены векторные обозначения: b ⁺ = (b₁,  b₂, …, b_p) –  вектор-строка (транспонированный вектор-столбец b);       X – вектор-столбец 

b ⁺X = êb₁,  b₂, …, b_p ê= b₀ + b₁X₁ + b₂X₂ + … b_pX _p.

                                                                                          (2.3.2)

Обозначим

COV⁺(Y,X) = {cov(Y,X₁), cov(Y,X₂), …, cov(Y,X_p)},       (2.3.3)

å = .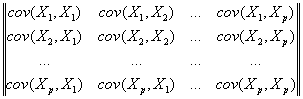

Тогда коэффициенты предиктора, минимизирующие ошибку (2.2.1) предсказания (см. также стр. 8), можно выразить в виде