Цифровые устройства и микропроцессорные системы. Задачи и упражнения: Учебное пособие (Представление чисел и арифметические операции в цифровых устройствах. Микропроцессорные устройства и системы на базе МП КР580ВМ80), страница 6

г) áAñ_доп = 01101010; á-Bñ_доп = 10101011; áAñ_доп + á-Bñ_доп =  100010101; áRñ_доп = 00010101; R= 0010101;

д) áAñ_доп = 01010101; á-Bñ_доп = 10010110; áAñ_доп + á-Bñ_доп =  11101011 = áRñ_доп ; R = - 0010101.

Р1.34. а) -0,10001111;           б) -0,0011111101;      в) 0,11100001;            г) 110110011.

Р1.35. а)

    D ≈ -0,1110;   остаток 0,00000101;

б) – 0,1010,     остатка нет;

в) – 0,1111,     остатка нет;

г) 10001, 011, остаток есть

Р1.36. а, б) Не более п + 1;  в) не более 2n;           г) не более п + т.

Р1.37. Суммирование чисел, представленных в двоично-десятичном коде 8421, выполняется в два этапа [28]. На 1-м этапе вычисляется предварительная сумма S_n, причем суммирование производится по обычным правилам двоичной арифметики, но со следующими уточнениями и дополнениями:

если в i-й тетраде S_niпредварительной суммы образуется естественный перенос, то он учитывается в следующей (i + 1)-й тетраде;

если в i-й тетраде S_niестественного переноса нет, но S_ni 10. то считается, что есть искусственный перенос, и он опять же учитывается в (i + 1)-й тетраде;

при S_ni < 10 переноса нет.

На 2-м этапе каждая тетрада S корректируется по следующему правилу:

если S_ni 10, т. е. в данной тетраде образовался естественный или искусственный перенос, то к ней прибавляется число 6: образующийся при этом перенос не учитывается. Ниже в примерах естественный перенос обозначается 1^е, искусственный – 1^и.

1^и             1^и

а) 0,597   0,0101   1001    0111

+       +   

0,346   0,0011   0100    0110______________________

0,943   0,1001   1110    1101 предварительная сумма

+

0000   0110    0110 коррекция

0,1001   0100    0011 сумма

1^и         1^е

б) 0,2098  0,0010   0000    1001   1000

+       + 

0,3729  0,0011   0111    0010   1001

0,5827   0,0101   1000    1100    0001

+

0000   0000    0110    0110

0,0101   1000    0010    0111

1^и        1^и

в) 0,3721   0,0011   0111    0010    0001

+       +

0,5683   0,0101   0110    1000    0011

0,9404   0,1001   1110    1010    0100

+

0000   0110    0110    0000

0,1001   0100    0000    0100

Глава 2. КОМБИНАЦИОННЫЕ ЦИФРОВЫЕ УСТРОЙСТВА

2.1. КОМБИНАЦИОННЫЕ ЦИФРОВЫЕ УСТРОЙСТВА НА ИНТЕГРАЛЬНЫХ ЛОГИЧЕСКИХ МИКРОСХЕМАХ

В данный раздел включены задачи и упражнения, связанные с анализом и синтезом комбинационных цифровых устройств на интегральных логических микросхемах [2, 3, 21].

При решении задач используются следующие соотношения булевой алгебры:

                         (2.1)                                 (2.2) 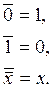      뎡                            (2.3.)

Основные законы:

перемесгительный закон

x Ú y = y Ú x, xy = yx;                                                                                                (2.4)

сочетательный закон

x Ú y Ú z = (x Ú y) Ú z = x Ú (y Ú z);                                                                         (2.5)

распределительный закон

x(y Ú z) = xy Ú xz;                                                                                                

x Ú yz = (x Ú y) (x Ú z);                                                                                             (2.6)

закон поглощения

x Ú xy =x, x(x Ú y) = x;                                                                                              (2.7)

закон склеивания

.                                                                                (2.8)

Правило де Моргана

, .                                                                                            (2.9)

Некоторые полезные соотношения:

,                                                                                                             (2.10)

,                                                                                                           (2.11)

,                                                                                                            (2.12)

.                                                                                                  (2.13)

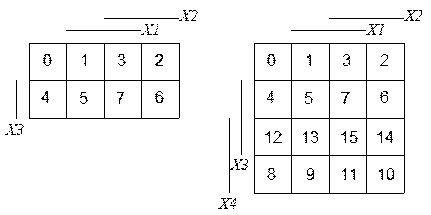
Рис. 2.1. Карты Карно для трех и четырех переменных