Р1.3. Целое число А в системе с основанием р имеет вид А=аn аn-1...аi...а2а1, где аi Î{0, 1, ..., р- 1}, i = 1,..., n; аi — неизвестные пока значения разрядов, т. е.
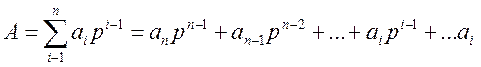
Последовательно деля А и полученные частные Bjна р, имеем:
А/р = ап р п - 2 + а n - 1 р n - 3 + ... + а 3 р + а2 = В1, остаток a1;
В1/р = а n р n - 3 + ап - 1 р п - 4 + ... + а3 = В2,, остаток а2;
Вn - 1/р = аn , остаток a n -1..
Таким образом, в остатке каждый раз получается соответствующий разряд числа в системе счисления с основанием р.
Р1.4.
Дробное число А
в системе счисления с основанием р имеет вид A =0, a1a2...ai...am, где аi — неизвестные пока значения разрядов, причем аi 
{0, 1, ...,p-1}, i = 1, ..., т. Следовательно,
A = a1 p- 1+a2 p-2+ ... + ат р- m.
Последовательно умножая это выражение и дробные части полученных произведений Сj на р, имеем
Ap = a1 +a2 p-1+a3 p-2 + .. +am p- m+1 = аl + C1;
C1 р = а2 + аз p- 1 + ... + ат р- m+ 2 = а2 + С2 ;
С т р т = ат.
Таким образом, целые части произведений являются соответствующими разрядами числа в системе счисления с основанием р.
Р1.5.
Для получения
абсолютной погрешности, не превышающей 
, необходимо иметь в
системе с основанием р такое число разрядов т, чтобы выполнялось соотношение
1/p m 
D, т.е.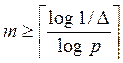 
Р1.6. Считаем, что абсолютная погрешность числа определяется единицей младшего разряда. Тогда для сохранения точности должно быть
1/pm1/qn, т. е. 
При q = 10, p = 2 должно быть m
3,3n.
Р1.7. а) 27(10) = 11011(2) = 1В(16);
б) 127(10) = 1111111(2) = 7F(16);
в) 74(10) = 1001010(2) = 4А(16).
Р1.8. a) D5(16) = 11010101(2) = 213(10); D5(16) = 13×16 + =213(10);
б) 127(16) = 0001 0010 0111(2) = 295(10); 127(1б)= 1×162 + 2×16 + 7 = 295(10);
в) E1(16) = 1110 0001(2) = 225(10);
г) CAB(16) = 1100 1010 1011(2) = 3243(10);
д) 11C2(16) = 0001 0001 1100 0010(2) = 4546(10).
Р1.9. а) 10101(2) = 25(8) = 2×8 + 5 = 21(10);
б)
1,101(2) = 1,5(8) = 1×80 + 5×8-1 = 
= 1,6250(10);
в) 10,0101(2) = 2,24(8) = 2×80 + 2×8-1 + 4×8-2 = 2,0625(10);
г) 1,11001(2) = 1,62(8) = 1,80 + 6×8-1 + 2×8-2 = 1,7813(10).
Р1.10. а)
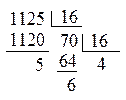1125(10)
= 465(16).
б)
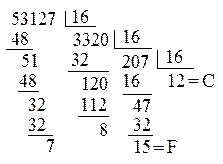53127(10) = CF87(16)
в)
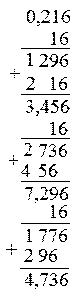0,216(10) » 0,374(16)
Р1.11. а) 1,001(2)=1×2° + 0×2-1+ 0×2-2 + 1×2-3 = 1,125(10);
б) 0,1011(2) 
0,688(10);
в) 101,1001 (2) = 5,563(10).
Р1.12. а) 23(10) = 27(8);
б) 1,25(10) = 1,2(8);
в) 100,57(10) = 144,4436(8)
(для получения заданной точности 0,001(10) необходимо иметь в дробной части восьмеричного числа четыре разряда).
Р1.13. 101110(16) > 101110(8) > 101110(2) .
Р1.14. а) 11111(2) = 25 – 1 = 31(10);
б) FFF(16) =163 – l = 4095(10);
в) 7777(8) = 84 – 1 = 4095(10);
г) (N + 1)n – 1.
Р1.15. а) 28(10) = 100000000(2);
б) (26 – 1)(10) = 111111(2);
в)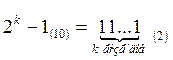 
Р1.16. а) 0,65(10) » 0,1010(2);
б) 23,625(10) = 10111,1010(2);
в) 1,217(10) » 1,0011(2).
Р1.17. Каждая цифра переводится независимо от других в 4-разрядный двоичный код:
а) 27(10) = 0010 0111(2/10) ;
б) 316(10) = 0011 0001 0110(2/10) ;
в) 4571(10) = 0100 0101 0111 0001(2/10);
г) 0101 1001(2) = 89(10) = 1000 1001(2/10).
Р1.18. Число делится на тетрады, и каждая тетрада независимо от других переводится в десятичный код:
а) 0010 0110(2/10) = 26(10) = 11010(2);
б) 1001 0010(2/10) = 92(10) = 1011100(2).
Р1.19. а) 01011010; б) 10101011; в) 11111001.
Р1.20. Предварительно число должно быть нормализовано.
а) 
В ячейке записано число 0,1010010×20 = 0,1010010.
б) 1110111000000101
В ячейке записано число — 0,1101110×25= -11011,10.
в) 0101101110000011
В ячейке записано число 0,1011011×2-3 = 0,0001011011.
Р1.21. а) Для целой части числа необходимо выделить v=élog2100(10)ù =7 двоичных разрядов, для дробной части m = éúlog0,1êù = 4 разряда. Учитывая знаковый разряд, всего получаем 12 разрядов:
б) 18; в) 28.
Р1.22. С учетом знаковых разрядов мантиссы и порядка:
а) 11; б) 13; в) 11; г) 16; д) 14.
Р1.23. Максимальное n-разрядное число при записи с фиксированной точкой – это целое положительное число AФмакс = -(2n - 1 – 1) (один разряд – знаковый). Минимальное число AФмин =-AФмакс = -(2n-1-1). Диапазон чисел Dф = AФмакс-АФмин = 2(2n-1-1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.