Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта

1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ УПРАВЛЕНИЯ

Нижеприведем математические модели динамических объектов управления (ОУ), чаще всего используемых при синтезе систем управления. Будем считать, что объект  одномерный, линейный, с сосредоточенными параметрами, без чистого запаздывания, устойчивый.

1.  Дифференциальное уравнение (ДУ)

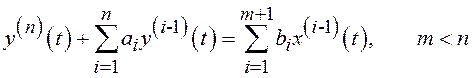          .                             (1.1)

Уравнению (1.1) при нулевых начальных условиях в объекте соответствует дробно-рациональная передаточная функция (ПФ)

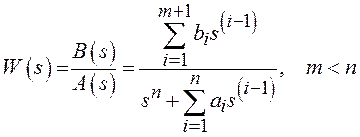,                                     (1.2)

- переменная Лапласа.                                               

ДУ (1) и ПФ (2) характеризуются одной и той же совокупностью параметров  ,    и в этом смысле представляют собой адекватные математические модели. Данные модели чаще всего используются при синтезе систем управления.

2.  Амплитудно-фазовая характеристика (АФХ).

Если в выражении (1.2) переменную Лапласа  заменить  на ,  - круговая частота, то будем иметь амплитудно-фазовую характеристику

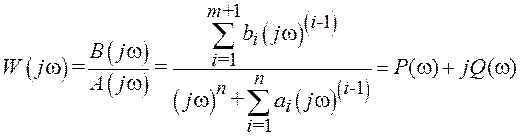.                               (1.3)

При решении практических задач чаще используются амплитудная (АЧХ)

                                   (1.4)

и фазовая (ФЧХ)

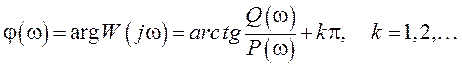                     (1.5)

частотные характеристики, - вещественная часть АФХ,  - мнимая часть АФХ, - четные функции частоты, - нечетные функции частоты.

3.  Интегральное уравнение свертки

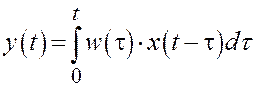                                           (1.6)

полностью определяется математической моделью в виде импульсной характеристики (ИХ) , удовлетворяющей условию физической реализуемости устойчивого объекта   при  , .

Следует отметить, что иногда вместо выражения (6) используется интегральное уравнение Винера-Хопфа

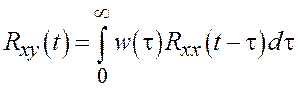,                                         (1.7)

где  ИХ связывает посредством интегрального оператора не сигналы, а корреляционные функции. Здесь

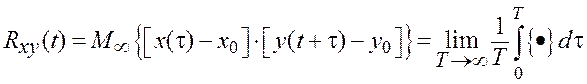
- взаимная корреляционная функция входного и выходного сигналов,

- автокорреляционная функция входного сигнала,

- математические ожидания входного и выходного сигналов.

Представленные три типа математических моделей взаимно связаны между собой посредством преобразований Лапласа и Фурье.

Связь между ИХ  и ПФ  осуществляется через пару преобразований Лапласа

,

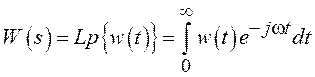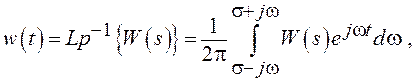
,    -  радиус сходимости.

Связь между ИХ  и АФХ  осуществляется через пару преобразований Фурье

,

.

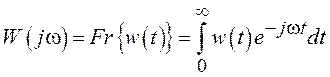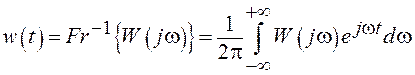4.  Разностное уравнение

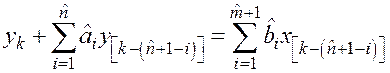,                                (1.8)

которому соответствует дискретная ПФ (ДПФ)

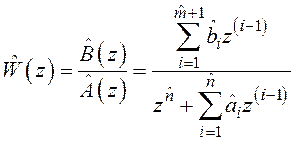,     ,                             (1.9)

 - шаг дискретизации по времени ().

Связь между ДПФ   и  ИХ  ,  ,  осуществляется парой -преобразования

,

.

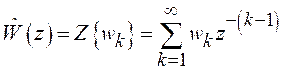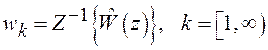2. ОБЩИЕ СВЕДЕНИЯ ОБ ИДЕНТИФИКАЦИИ

Идентификацией объекта управления (ОУ) будем называть процедуру определения математической зависимости между входным  и выходным  сигналами ОУ (рис. 1) на основе обработки этих сигналов. Указанная зависимость и будет представлять собой математическую модель данного объекта.

Рис. 2.1

Математическая модель служит для оценивания и прогнозирования ненаблюдаемых переменных состояния объекта, прогнозирования наблюдаемых переменных, расчета стратегии управления. В качестве иллюстрации постановки задачи идентификации и определения математической модели рассмотрим некий линейный стационарный динамический объект, который описывается дифференциальным уравнением (ДУ) вида

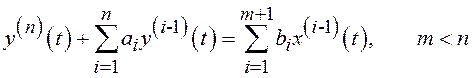          .                             (2.1)

Необходимо определить порядки  и  левой и правой частей ДУ и коэффициенты ,   .

Априорной информацией для решения задачи идентификации являются измеренные (как правило, с помехами) входной  и выходной  сигналы объекта подлежащего идентификации.

Наличие аддитивных помех  и , использование численных методов в алгоритмах идентификации (методическая погрешность), обработка информации на ЦВМ (вычислительная погрешность) приводят к тому, что результатом решения задачи идентификации будут лишь оценки искомых параметров математической модели ,

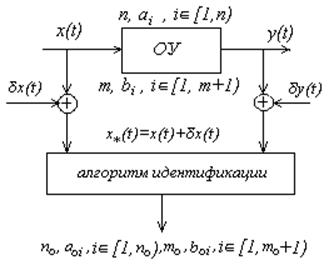
Рис. 2.2

Помехи  и  возникают по причине преобразования сигналов любой физической природы в электрические сигналы вида удобного для обработки на ЦВМ. Цепочку преобразования можно представить в следующем виде: датчик (первичный преобразователь)  нормирующее устройство  АЦП  буфер памяти. Все эти устройства несовершенны и вносят искажения в процессе преобразования. Кроме того может оказывать влияние и окружающая среда в виде каких-либо возмущающих воздействий.

      

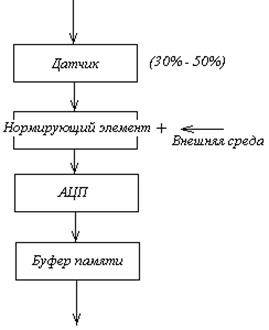
Рис. 2.3

Идентификация называется активной, если входной сигнал  - тестовый (подается на объект со специального генератора). Если же он измеряется в процессе нормального функционирования объекта, то имеет место пассивная идентификация.

Определение порядков левой  и правой  частей ДУ называют структурной идентификацией, а определение коэффициентов , и – параметрической идентификацией. Это касается и передаточной функции (ПФ) , где  и  - порядок и коэффициенты полинома знаменателя , а  и  - порядок и коэффициенты полинома числителя  ПФ.

Задачи определения импульсной характеристики (ИХ) , амплитудной (АЧХ)  и фазовой (ФЧХ)  частотных характеристик  называются непараметрической идентификацией.