Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 15

Таким образом, с точки зрения точности приближения необходимо использование полиномов Чебышева и в этом смысле различие между способами приближения теряется.

В плане решения практических задач, когда приближаемая функция представлена в виде зашумленной реализации сигнала, предпочтительнее среднеквадратическая аппроксимация. Во-первых, как теория она имеет наиболее простой и законченный вид. Во-вторых, среднеквадратическая близость, за счет наличия интегрального оператора, учитывает погрешность приближения на всем интервале аппроксимации, а не в точке, а кроме того интегральный оператор обладает сглаживающими свойствами. Следовательно, представляется целесообразным, отдать предпочтение среднеквадратической аппроксимации, а именно обобщенному ряду Фурье по ортонормированным полиномам Чебышева первого рода.

Полиномы Чебышева первого рода  ортонормированны на интервале  с весом

.

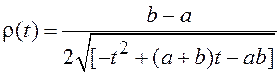Вычисление коэффициентов Фурье при аппроксимации функции

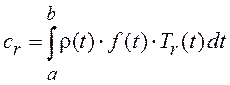
предполагает использование квадратурных формул с реализацией их на ЦВМ. Однако в точках  и  весовая функция обращается в , поскольку в этих точках знаменатель  равен нулю и вычисление коэффициентов Фурье невозможно. Вручную, подобного рода интегралы не берутся, особенно если  задана не в аналитическом виде.

Исследования, проведенные на предмет использования другого, близкого к полиномам Чебышева базиса, проиллюстрировали неплохие результаты, когда в качестве ортонормированного базиса брались близкие по виду и свойствам полиномы Лежандра , ортонормированные на интервале  с весом . 

Таким образом, вопросы выбора способа приближения и вида базисных функций решены в пользу обобщенного ряда Фурье по полиномам Лежандра.

Восстановление идентифицируемых параметров осуществляется по найденным оценкам нестационарных спектральных характеристик (оценкам коэффициентов Фурье). Ошибки определения искомых параметров возникают по следующим причинам.

Во-первых, в условиях задачи идентификации аппроксимируемые функции  неизвестны, следовательно, неизвестны априори и остаточные члены ряда Фурье . В результате вектор  оказывается неизмеримым, и решать возможно только усеченную систему

,                                               (9.8)

решение которой представляет собой оценку вектора , а значит  удается определить лишь оценки искомых нестационарных параметров

,  .   

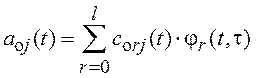В результате имеем методическую погрешность идентификации 

.

Во-вторых, с учетом помех , возникающих при измерении сигналов , система (9.8) принимает вид

,                               (9.9)

где

,

,

,

.

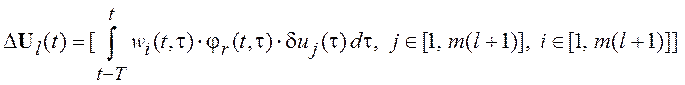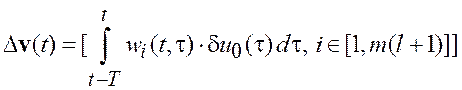Восстановление оценок  идентифицируемых параметров осуществляется по оценкам  нестационарных спектральных характеристик, полученных в результате решения системы (9.9), причем это восстановление может быть произведено либо сразу на всем интервале аппроксимации, либо в отдельной точке этого интервала. Текущая идентификация предполагает информацию о свойствах и поведении наблюдаемого объекта в момент времени , что представляет собой точку правого конца интервала аппроксимации и, логически, именно эту точку, казалось бы,  необходимо выбирать в качестве точки восстановления. Однако, как показывают многочисленные модельные исследования, хорошо вписывающиеся в рамки свойств полиномов Лежандра (впрочем как и Чебышева), ошибка идентификации минимальна при восстановлении идентифицируемых параметров в точке

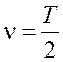,                                                     (9.10)

т.е. в середине интервала аппроксимации. Именно в этой точке полиномы Лежандра с нечетными индексами обращаются в нуль, что, вообще говоря, определяет и значение параметра  - количества слагаемых ряда Фурье. Недостатком выбора точки восстановления в виде (9.10) является вносимое в  текущую идентификацию таким выбором запаздывание на величину . В результате можно дать следующую рекомендацию по выбору точки . Если предъявляются более жесткие требования к информации об объекте именно в данный момент времени, пусть даже в ущерб точности этой информации, то следует полагать . Если же функционирование объекта в том технологическом процессе, где он используется, допускает небольших запаздываний, но требует более точной информации о свойствах объекта, то точку восстановления рекомендуется выбирать в виде (9.10).