Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 3

Соотношение (3.6) представляет собой основу, так называемых, прямых методов идентификации, в том числе и метода наименьших квадратов (МНК).

Соотношение (3.6) на конечном интервале , , ,  представляет собой систему  линейных алгебраических уравнений относительно  неизвестных. Параметр  указывает, сколько раз длительность ИХ   укладывается на отрезке  наблюдаемых сигналов  входа и выхода объекта идентификации. В векторно-матричной форме данная система имеет вид

,                                                   (3.7)

где                                               ,

,

,

.

Вектор обобщенной помехи  оказывается неизмеримым и решение системы (3.7) методом наименьших квадратов предполагает минимизацию функционала

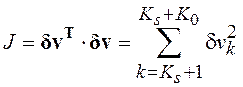,                                           (3.8)

что приводит к усеченной системе

относительно оценок  ИХ  и после первой трансформации Гаусса окончательно имеем

,      .                                      (3.9)

Формально, решение системы (3.9) может быть представлено в виде

,                                                (3.10)

что является МНК – оценкой искомого вектора ИХ.

          Представим систему (3.7) следующим образом

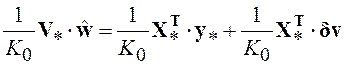                                 (3.11)

и вводя в рассмотрение оценки корреляционных функций

,

,

перейдем к эквивалентной системе уравнений

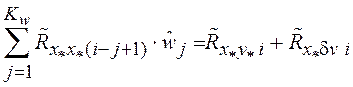,   ,                       (3.12)

вид которой понадобится в дальнейшем для целей ее анализа.

Следует отметить, что корреляционные функции могут определяться для стационарных процессов, поэтому возникает условие , гарантирующее близость сигнала  к стационарному процессу. Кроме того, параметр , определяющий длительность интервала усреднения (величину ) нужно брать как можно больше, поскольку с увеличением  оценки корреляционных функций будут приближаться к истинным.

Корректирующими параметрами, определяющими эффективность МНК идентификации ИХ, АЧХ, ФЧХ, являются шаг дискретизации по времени , длительность ИХ   (), длительность интервала наблюдения (усреднения) , определяемая параметром .

Анализ МНК, что ошибка идентификации

                                       (3.13)

зависит от обусловленности матрицы, определяемой числом Тодда

, где   и    - максимальное и минимальное собственные числа матрицы  (чем больше , тем хуже обусловленность) и содержит методическую и инструментальную составляющие.

Обусловленность матрицы  может ухудшаться по двум причинам.

Первая причина связана с увеличением мерности матрицы , которая определяется количеством искомых параметров . Следовательно, чтобы улучшить обусловленность  матрицы  необходимо либо уменьшать эффективную длительность ИХ , либо увеличивать шаг дискретизации . И то и другое приводит к увеличению уровня обобщенной помехи .

Вторая причина порождается недостаточной информативностью входного сигнала на объект идентификации. Входной сигнал считается информативным, если выполняется условие , где - максимальная частота эффективной длительности спектра входного сигнала, а  - максимальная частота эффективной длительности АЧХ объекта.

Методическая составляющая ошибки идентификации  возникает из-за наличия обобщенной помехи (3.5), куда входят слагаемые  от усечения ИХ

и погрешности  квадратурных формул. Причем ошибка будет уменьшаться при уменьшении , что связано с увеличением , а уменьшение ошибки  связано с уменьшением , что в свою очередь будет иметь место при уменьшении  или . Таким образом, из-за противоречивого влияния параметров  и  методическая составляющая ошибки идентификации не может быть уменьшена ниже некоторого граничного значения, величина которого возрастает с увеличением  (). Отсюда следует, что МНК применим при идентификации слабо колебательных ИХ, характеризуемых малыми значениями  при больших величинах .   

Инструментальная составляющая ошибки (3.13) связана с наличием помех  и , искажающих входной  и выходной  сигналы идентифицируемого объекта. Уменьшение этой ошибки может быть обеспечено за счет соответствующего выбора генератора входного сигнала, измерительной и регистрирующей аппаратуры, а также за счет увеличения интервала усреднения . Указанные требования приводят к тому, что в обобщенной помехе (см. (3.11)) ,  (выбор аппаратуры), а увеличение параметра  обеспечивает приближение оценок  к их истинным значениям.