Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 11

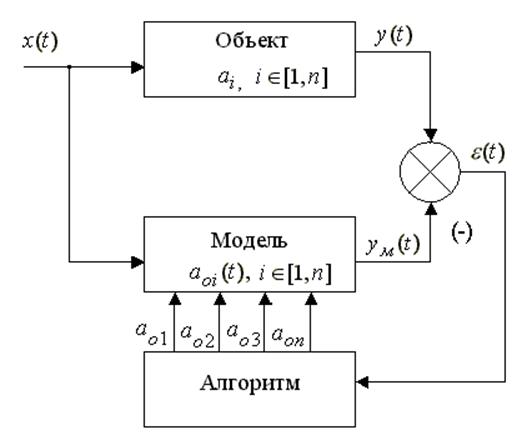
(на слайдах не хватает минуса на сумматоре)

Рис. 6.1 Структурная схема системы идентификации с ГСМ

Априори предполагается, что существует

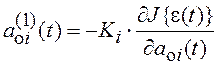,   ,    ,                             (6.1)

где  - выбираемый критерий настройки модели по параметрам .

Если предположение (6.1) выполняется то алгоритм идентификации (подстройки параметров модели к параметрам объекта) имеет вид

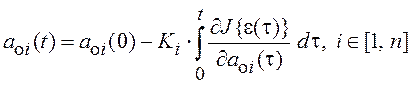,                            (6.2)

где  - задаваемые начальные условия параметров модели.

В качестве иллюстрации функционирования ГСМ  рассмотрим пример.

Пусть идентифицируемый объект описывается уравнением

.

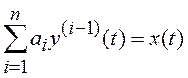Дифференциальное уравнение модели

.

          Критерий настройки параметров модели к параметрам объекта выберем в виде

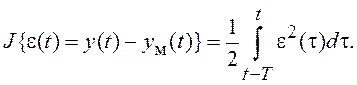
Тогда, в предположении, что на интервале длительностью (этапе подстройки параметров модели)    

 , можно записать

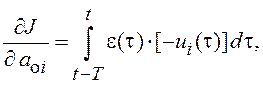
где

,    

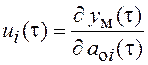называются функциями чувствительности модели по ее параметрам и представляют собой решение дифференциального уравнения чувствительности

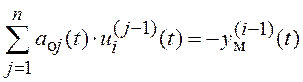,  , с нулевыми  начальными условиями

 

При этом алгоритм идентификации (6.2) принимает вид

,     .

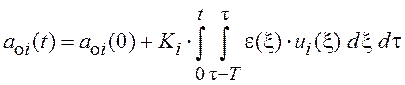Корректирующими параметрами алгоритма являются время усреднения , коэффициенты , , корректирующие динамику системы, начальные условия , .

Достоинством ГСМ является тот факт, что это система замкнутого типа и потому, если выходной сигнал  объекта искажен центрированной и не коррелирующей с  помехой , то ее наличие не приводит к смещенности оценок .

Недостатки ГСМ.

1. ГСМ описываются системой нелинейных, нестационарных, интегро-дифференциальных уравнений, заданных в неявном виде и потому не представляется возможным провести необходимый теоретический анализ не только точности и быстродействия, но даже устойчивости.

2. Как правило критерии настройки  не унимодальные и потому сходимость параметров модели  к  параметрам объекта , будет иметь место, если начальные условия ,  достаточно близки к параметрам объекта ,, а это связано с необходимостью наличия дополнительной априорной информации.

3. Функции чувствительности  являются функциональными производными и их определение через модели чувствительности справедливо только при очень медленном изменении параметров модели ,. Поэтому ГСМ имеют принципиально низкое быстродействие.

4. ГСМ характеризуются сильной взаимной связью между каналами идентификации. Поэтому с увеличением количества  подстраиваемых параметров быстродействие резко падает.

6.2. НЕ ГРАДИЕНТНЫЕ САМОНАСТРАИВАЮЩИЕСЯ МОДЕЛИ

Структурная схема системы идентификации с  не градиентной самонастраивающейся моделью (НГСМ) представлена на рис.7.1.

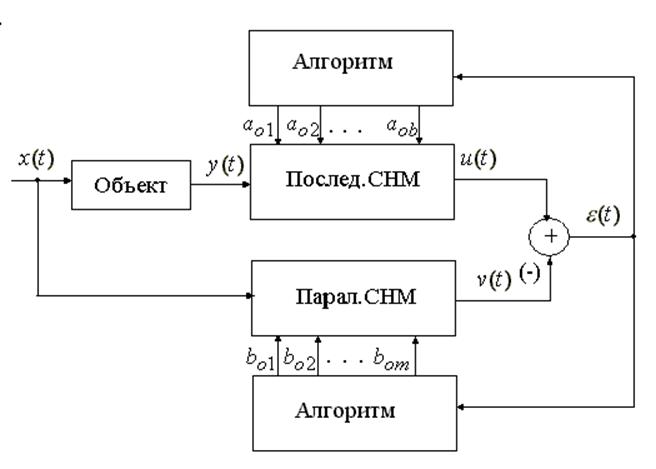
Рис. 6.2 Структурная схема системы идентификации с НГСМ

Пусть объект описывается уравнением

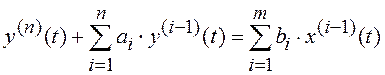.                              (6.3)

Последовательная модель имеет вид

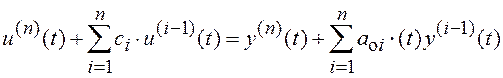,                   (6.4)

а параллельная

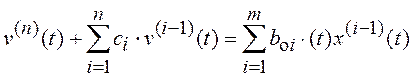.                           (6.5)

Коэффициенты ,  последовательной и параллельной моделей задаются априори из условия их устойчивости, а при необходимости и из дополнительных условий, например, обеспечения требуемой полосы пропускания параллельной модели для сглаживания помех.

Если ввести в рассмотрение: рассогласование    

, ошибку по параметрам последовательной модели

, ошибку по параметрам параллельной модели

, то динамику НГСМ  можно описать системой дифференциальных уравнений

.

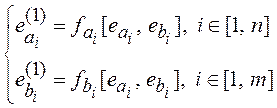Алгоритм идентификации синтезируется из условий устойчивости

  и   , а в качестве критерия устойчивости можно использовать, например, второй метод Ляпунова или гиперустойчивости Попова.

При использовании второго метода Ляпунова выбирается функция Ляпунова, например, в виде

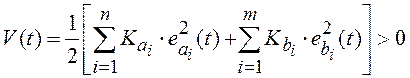,                      (6.6)

где  и  определяют скорость сходимости алгоритма и задаются из условия коррекции динамики системы идентификации, причем, , ,  и, в частности, их можно положить равными единице.

Согласно критерия Ляпунова устойчивость будет иметь место, если

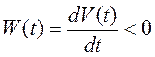.                                            (6.7)

Определим вспомогательную функцию , которая получается при почленном вычитании уравнения (7.3) из уравнения (7.2)

.

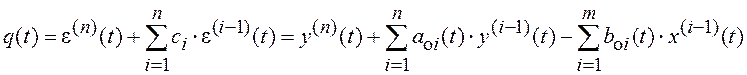В полученном выражении заменим