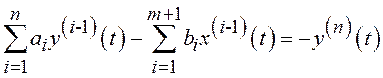Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 6

,                             (4.4)

а совокупность  функций ,  образуют систему линейно зависимых функций, т.к.

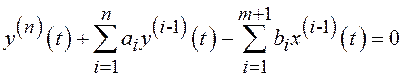.                           (4.5)

В результате, если посредством какого либо критерия непосредственно или апосредованно определяется факт перехода от системы линейно независимых функций (4.4) к линейно зависимой системе (4.5) при  и , то полагается , .

Сложность использования ранговых критериев обусловлена наличием помех, а также методических и вычислительных ошибок, что приводит к проблеме определения нуля, который свидетельствует о переходе к линейно зависимой системе функций.

При использовании информационных критериев оценки порядков  и  отыскиваются в рамках  – процедуры в виде  и , где  и  определяются из условия

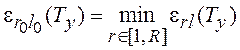.                                           (4.6)

Проверка статистических гипотез используется в основном при оценивании параметров авто регрессионных (АР) и авто регрессионных скользящего среднего (АРСС) моделей, когда в качестве априорной информации используется только выходной сигнал объекта в предположении, что на его входе случайный сигнал типа «белый шум» с известной дисперсией.

4.3. Структурная идентификация объекта

по оценке его импульсной характеристики

Предлагаемый подход к оцениванию структуры и параметров базируется на восстановлении РУ (дискретной ПФ), а затем и  ДУ (непрерывной ПФ) по оценке ИХ, т.е. в данном случае в качестве априорной информации используются не сигналы входа и выхода объекта, а предварительно идентифицированная ИХ.

Достоинства данного подхода по сравнению с ранее рассмотренными в следующем.

1. Нет необходимости измерения производных входного и выходного сигналов объекта, что вообще  говоря, представляет весьма существенную проблему.  Решение же задачи идентификации ИХ не требует наличия производных в качестве априорной информации.

2. Известны (см. раздел 3) высоко эффективные алгоритмы идентификации ИХ, которые оказываются малочувствительными к степени колебательности ИХ  объекта и обладают высокой помехоустойчивостью. В результате, помехи высокого уровня, искажающие реализации входного и выходного сигналов объекта, трансформируются в помеху существенно меньшего уровня, искажающую идентифицируемую оценку ИХ. Например, модифицированный МНК идентификации ИХ дает относительную среднеквадратичную ошибку  порядка 0,06 при широкополосной помехе уровня относительно максимального значения выходного сигнала  на интервале наблюдения. 

Основной недостаток метода, базирующегося на восстановлении РУ и ДУ  – предварительная идентификация ИХ объекта.

Таким образом, задачу сформулируем в следующем виде. Требуется оценить порядки и коэффициенты полиномов числителя и знаменателя дискретной  ПФ  (1.9), а в качестве априорной информации использовать  реализацию оценки  ИХ  , заданной  отсчетами  с шагом , . Дополнительно предполагается известной оценка верхней частоты  эффективной полосы АЧХ объекта, которая, вообще говоря, определяется в процессе идентификации ИХ.

Решение поставленной задачи осуществляется на базе  – преобразования

.                                     (4.7)

Связь между отсчетами   реализации ИХ и коэффициентами полиномов  и  может быть представлена в виде

, при ,

, при ,

,

.

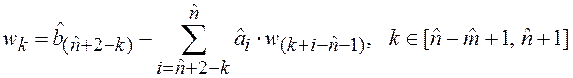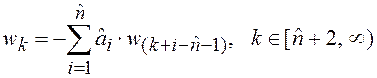Данные выражения, по существу, представляют собой расчетные формулы обратного  – преобразования, которые для нашей задачи удобнее преобразовать  к следующему виду

,  при  ,                                 (4.8)

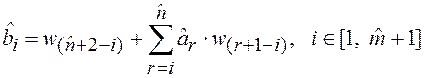,                          (4.9)

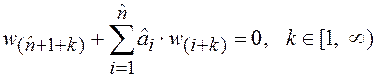.                            (4.10)

Из соотношения (4.10) следует, что на любом конечном  или бесконечном  множестве функции  образуют систему  линейно независимых функций, а функции  – линейно зависимую систему.

Далее, как и в ранее рассмотренной  – процедуре, производится перебор порядка , т.е. на каждом – том шаге  () формируется однородное уравнение

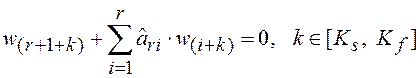
и проверяется линейная зависимость функций . Если на некотором  – м шаге  стали линейно зависимыми, то

.                                                     (4.11)

Здесь, как и в  – процедуре возникает проблема определения линейной зависимости функций.