Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 14

  при   ,                                         (9.3)

где  -  некоторая конечная фиксированная величина.

Решение интегрального уравнения Вольтера (9.2) представляет собой некорректную задачу и известные методы, в том числе и регуляризация по А.Н. Тихонову, оказываются мало пригодными в условиях текущей идентификации.

Для решения системы (9.2) предлагается метод, в основе которого лежит представление идентифицируемых параметров на скользящем интервале времени  в виде обобщенного ряда

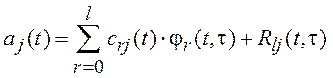,                         (9.4)

 - коэффициенты приближения (нестационарные спектральные характеристики),

 - базисные функции обобщенного ряда,

 - остаточный член обобщенного ряда.

С учетом (9.3) система (9.2) представляется как

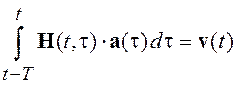.                                           (9.5)

Подставляя (9.4) в (9.5) получим эквивалентную систему алгебраических уравнений относительно нестационарных спектральных характеристик

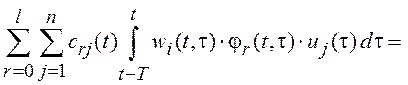
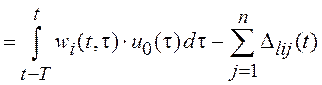,  ,                       (9.6)

где  .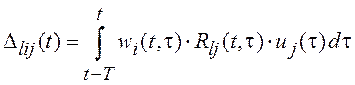

Система (9.6) может быть записана в векторно-матричной форме

,                                       (9.7)

,

,

,

.

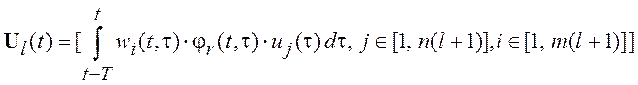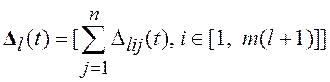Если предположить, что остаточные члены известны, а тем самым известен и вектор , то, при условии не вырожденности матрицы , описанная процедура позволит определить истинные параметры , .

Следует отметить основное достоинство описанного подхода к идентификации нестационарных параметров, которое заключается в том, что решение интегральной системы (9.5) сводится к решению линейной алгебраической системы (9.7), формируемой на интервале , а это существенно упрощает задачу, поскольку определяемые из системы (9.7) коэффициенты  (вектор ) постоянны на .

Однако при этом имеет место и основной недостаток – существенное увеличение мерности решаемой задачи, т. к. теперь вместо  параметров , , необходимо определять  коэффициентов ,.

Реализация алгоритма предполагает решение следующих вопросов.

1. Выбор вида формирующих функций .

2. Выбор способа приближенного представления идентифицируемых параметров (обобщенного ряда (9.4)).

3. Выбор вида базисных функций .

4. Выбор способа восстановления параметров  по идентифицированным оценкам .

Вопрос выбора функций , формирующих систему линейных алгебраических уравнений, обсуждался в разделе 5.1. Аналогичная ситуация имеет место и здесь, т.е. в качестве формирующих функций  следует выбирать ИХ полосовых фильтров с разнесенными полосами пропускания, расположенными в пределах эффективной длительности АЧХ  идентифицируемого объекта. Однако в отличие от стационарного случая формирование системы уравнений здесь осуществляется на интервале , т.е. длительность  ИХ полосового фильтра и длительность  скользящего интервала должны быть согласованы. С точки зрения приближения функций, чем меньше , тем меньше ошибка приближения и  надо уменьшать. С другой стороны длительность  ИХ определяет качество АЧХ полосового фильтра, причем, чем больше , тем выше качество  АЧХ и с этой точки зрения  надо увеличивать. Таким образом, конкретных рекомендаций по выбору  пока дать невозможно, по крайней мере до тех пор пока не будут обсуждены вопросы реализации способа приближения идентифицируемых параметров, а далее возможны варианты выбора либо по приоритету (что важнее) либо компромиссное решение.

По вопросу выбора способа приближенного представления идентифицируемых параметров остановимся на таких методах теории приближения функций как интерполирование, наилучшее равномерное приближение и среднеквадратическая аппроксимация.

Интерполяционный полином, обеспечивающий минимальную ошибку приближения – есть полином Лагранжа с узлами по Чебышеву.

В качестве одного из вариантов полинома наилучшего равномерного приближения рекомендован интерполяционный полином Лагранжа с узлами по Чебышеву.

Наилучшую среднеквадратическую аппроксимацию обеспечивает обобщенный ряд Фурье с полиномами Чебышева в качестве базисных функций, причем этот ряд в нашем случае обладает не только среднеквадратичной, но и равномерной сходимостью, поскольку приближаемые функции , .