Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 7

Однако если сравнивать сложность рассмотренного подхода и  – процедуры, то в данном случае отсутствует перебор структуры модели по параметру .

5. ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ

 ЛИНЕЙНОГО СТАЦИОНАРНОГО ОБЪЕКТА

5.1. Идентификация ЛНД – модели

ЛНД – модель идентифицируемого объекта будем представлять в виде

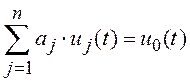,                                           (5.1)

где  – идентифицируемые параметры, а  – координаты объекта. Подобного вида модель может быть получена, если в ДУ

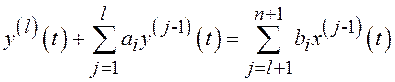
ввести обозначения

,   ,

,   ,

.

Ставится задача определить коэффициенты  уравнения (5.1) в предположении, что порядок  и координаты , известны.

Решение поставленной задачи будем отыскивать путем формирования системы  линейных алгебраических уравнений. Осуществляется это следующим образом. Слагаемые уравнения (5.1) умножим на некоторые линейно независимые функции  и проинтегрируем на интервале . Получим

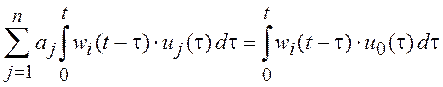,                       (5.2)

или

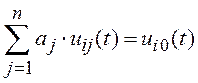,    .                                     (5.3)

Физически это означает (см. рис. 5.1),

 

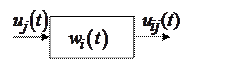
Рис. 5.1

что координаты  пропускаются через некие фильтры с ИХ  , на выходе которых получаем элементы матрицы  и вектора правой части   системы линейных алгебраических уравнений

,

,      ,     , которая при   выглядит как

.                                                      (5.4)

Поскольку может выполняться условие , то система (5.4) преобразуется к виду

,                                               (5.5)

а ее решение

                                            (5.6)

может быть получено при условии не вырожденности матрицы , что обеспечивается за счет:

1) линейной независимости координат ,  , для чего входной сигнал объекта должен содержать не менее  гармонических составляющих,

2) линейной независимости функций ,  .

Следует отметить весьма существенную проблему, возникающую в описанном методе идентификации, впрочем, как и в других случаях оценивания параметров ЛНД – объекта, связанную с информацией о производных входного и выходного  сигналов. Указанные производные входят в состав координат , а фактически можно измерить лишь только сами сигналы. В результате приходится прибегать к искусственным приемам, позволяющим избежать операции дифференцирования зашумленных сигналов. Одним из таких приемов является известное в математике интегрирование по частям. Напомним это правило.

.

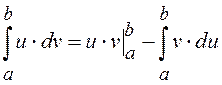В нашем случае имеем, например,

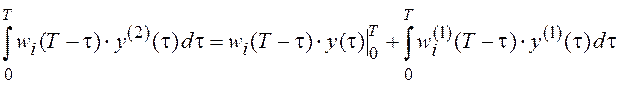, т.к.                                   ,

      

и далее

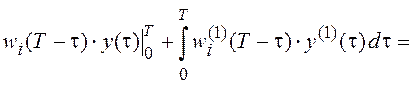
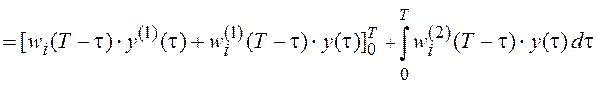, поскольку

.                                   ,

         .

В общем случае  выражение интегрирования по частям, позволяющее избежать операции дифференцирования сигналов, выглядит следующим образом

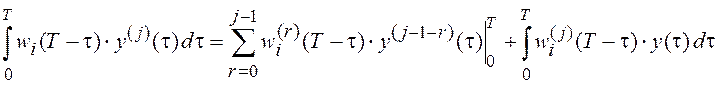.    (5.7)

Для обеспечения корректности описанного подхода, помимо требований, предъявляемых к  функциям , необходимо выполнение соотношения

,     ,                               (5.8)

что позволяет обеспечить

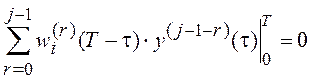.                                  (5.9)

Корректирующими параметрами, влияющими на ошибку идентификации, являются:

1) вид функций , формирующих алгебраическую систему, 

2) длительность  интервала интегрирования,

3) количество  формируемых уравнений.

Указанные параметры определяют свойства матрицы  формируемой системы уравнений, в частности ее обусловленность, анализ которой позволил дать рекомендации по выбору корректирующих параметров.

Линейная независимость строк алгебраической системы (5.5) будет выполняться наилучшим образом, если АЧХ ,  формирующих звеньев с ИХ   будут представлять собой АЧХ полосовых фильтров с разнесенными полосами пропускания в диапазоне частот эффективной длительности АЧХ идентифицируемого объекта, как показано на рис. 5.2.

Рис. 5.2

Выполнение указанного условия позволит устранить постоянную и высокочастотную составляющие помех, искажающих координаты , что положительно влияет на помехоустойчивость алгоритма идентификации.

Влияние параметра на свойства матрицы таково, что с увеличением  обусловленность матрицы  становится лучше, поскольку при этом усиливаются сглаживающие свойства интегрального оператора.