Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 16

10. ДИАГНОСТИКА ТЕХНИЧЕСКИХ ОБЪЕКТОВ

Задачами технической диагностики объектов являются:

1) определение работоспособности объекта;

2) поиск неисправностей (дефектов) в объекте;

3) прогнозирование изменения состояния объекта.

Решение указанных задач осуществляется с помощью систем диагностики, которые в общем случае можно представить в виде объекта диагностирования, средства диагностирования и оператора, которым может быть либо человек, либо специализированное устройство.

Эффективность функционирования систем диагностики зависит от контролепригодности объекта (пригоден ли он для оценивания состояния), что должно быть заложено при проектировании объекта.

О состоянии объекта можно судить, если ответить на два вопроса: «Что проверять?» и «Как проверять?». Ответы на эти вопросы могут быть получены на основе анализа модели объекта, которая отражает его свойства, особенности и изменения в состоянии объекта. В качестве таких моделей могут использоваться обычные математические модели такие как, например,  дифференциальные или  разностные уравнения, передаточные функции и т. д. Иногда, в зависимости от типа объекта диагностирования, необходимы специальные модели, пригодные только для целей технической диагностики.

В процессе исследования диагностической модели необходимо определить:

1) перечень оцениваемых диагностических показателей;

2) методы их оценивания;

3) условия работоспособности;

4) признаки наличия дефектов;

5) алгоритмы и программу диагностирования.

Совокупность этих данных будем называть диагностическим обеспечением.

Нормальное функционирование системы технической диагностики предполагает наличие математической модели диагностируемого объекта и диагностического обеспечения.

Математическая модель объекта – это результат решения задачи идентификации, которая может быть решена посредством методов и алгоритмов идентификации рассмотренных выше. Другими словами говоря, математическая модель диагностируемого объекта известна.

Что же касается диагностического обеспечения, то, для наглядности, рассмотрим, как определяются составляющие диагностического обеспечения на конкретном примере.

Пусть диагностируемый объект представляет собой двигатель постоянного тока с независимым возбуждением, управляемый напряжением на его якоре. Математической моделью такого двигателя служит дифференциальное уравнение

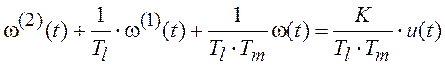, где  - напряжение на якоре двигателя;

 - угловая скорость вращения вала двигателя;

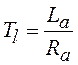 - электромагнитная постоянная времени, причем  и  - индуктивность и активное сопротивление якорной обмотки;

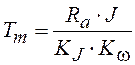 -  электромеханическая  постоянная  времени,  причем   и  - конструктивные константы двигателя.

В результате решения задачи идентификации математическая модель двигателя представляется в виде

, где входной  и выходной  сигналы измерены, а параметры ,  ,   - получены в процессе идентификации.

Далее формируется система, в общем случае, нелинейных алгебраических уравнений

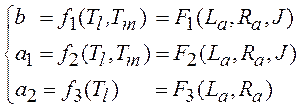, решая которую можно определить физические параметры объекта ,  и .

Данные параметры в рассматриваемой задаче представляют собой оцениваемые диагностические показатели, а метод оценивания – есть алгоритм решения алгебраической системы.

Условие работоспособности объекта можно выразить через допуски разброса параметров, например,

,

, где  и  - номинальные параметры, а  и  - те допустимые значения, превышение которых приводит к неисправности физического элемента.

Признаком наличия дефекта в объекте является скачкообразное изменение физических параметров двигателя, а, соответственно, и параметров математической модели объекта.

Алгоритм и программа диагностирования включают в себя методы идентификации и решения системы нелинейных алгебраических уравнений.