Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 10

Рис. 5.5.1. АЧХ звеньев и объекта

Рис. 5.5.2. зависимость от параметра К

Решение алгебраической системы обычным МНК запишем как

,     

и тогда численную реализацию РМНК можно поэтапно представить в следующем виде.

1. Задание начальных условий

,     ,     .                             (5.34)

2.  - шаговая итерационная процедура, на каждом  - ом шаге которой () вычисляются:

1)  оценка обратной матрицы

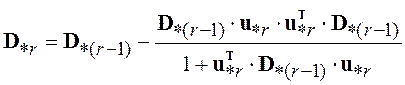,                            (5.35)

2) оценка вектора искомых параметров

,                                      (5.36)

где

.

Если рекуррентный алгоритм сходится, то при   .

Приведенный выше РМНК называют классическим алгоритмом. Чаще на практике используется РМНК с взвешиванием, отличающийся вычислением матрицы , а именно

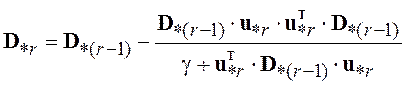,                        (5.37)

где вводится дополнительный параметр , характеризующий степень забывания старой информации (при  вся информация используется полностью).

Рис.5.5.3. влияние на ошибку

Новые корректирующие параметры РМНК: ,  ,  , причем в отличие от  и  существует проблема выбора параметра.

5.6. Алгоритм Качмажа

Здесь, как и в РМНК, используется итерационная процедура определения идентифицируемых параметров. Суть АК в следующем.

Задается начальное значение оценки вектора параметров. Обычно полагается

,                                                       (5.38)

а далее производится итерационная процедура уточнения, на каждом -ом шаге которой () возникает -ое уравнение

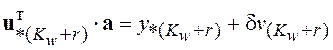,                                (5.39)

минимизируется функционал

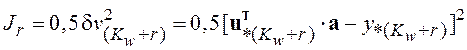, в результате чего вычисляется -ая оценка  вектора  в виде

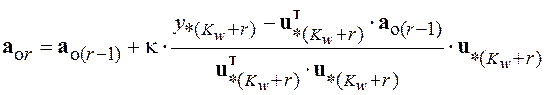,             (5.40)

где .

Выражение (5.40) называют классическим АК. На практике чаще используется алгоритм Качмажа – Чадеева (АКЧ)

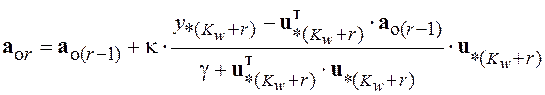,            (5.41)

где параметр  вводится для улучшения помехоустойчивости алгоритма.

5.7. Метод инструментальной переменной

В МИПсформированнаяв МНКалгебраическая система

преобразуется к виду

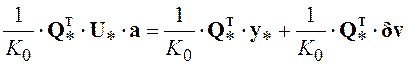.                         (5.42)

Матрица

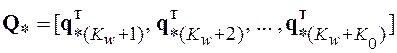
(не соответствуют буквы и часть текста)

формируется из отсчетов реализации функции , которая называется инструментальной переменной и которая должна удовлетворять двум требованиям.

1. Сильно коррелировать с элементами вектора , что обеспечивает не вырожденность матрицы .

2. Не коррелировать с обобщенной помехой , что при больших  приводит к выполнению условия

.

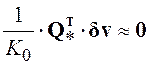Выполнение этих требований приводит к проблеме выбора вида инструментальной переменной. В литературе […], при условии, что помеха  на входном сигнале отсутствует, предлагается два подхода к выбору инструментальной переменной.

В методе сдвига инструментальная переменная выбирается в виде

, причем сдвиг  должен быть таким, чтобы сигнал  не коррелировал с обобщенной помехой . Однако никаких рекомендаций по выбору параметра  не дается.

Экспериментальные исследования с различными объектами идентификации проиллюстрировали следующие факты. Взаимная корреляционная функция близка к автокорреляционной ( при ) и это, практически, означает выполнение первого требования. А вот взаимная корреляционная функция  при , что свидетельствует о наличие корреляции инструментальной переменной с обобщенной помехой.

В методе линейного фильтра инструментальная переменная вычисляется посредством итерационной процедуры, на каждом -ом шаге которой

, а  есть оценка ПФ идентифицируемого объекта с параметрами , . При , в качестве начальных условий, берутся МНК - оценки , полученные обычным МНК.

Модельные исследования метода линейного фильтра иллюстрируют незначительное уменьшение степени корреляции инструментальной переменной как с сигналом  так и с обобщенной помехой  и в этом смысле метод линейного фильтра обладает преимуществом по сравнению с методом сдвига. Однако сходимость итерационной процедуры метода линейного фильтра не доказана и уменьшение ошибки идентификации от влияния неизмеримого вектора  обобщенной помехи носит случайный характер при изменении количества итераций.  

6. ГРАДИЕНТНЫЕ САМОНАСТРАИВАЮЩИЕСЯ МОДЕЛИ

Структурная схема системы идентификации с градиентной самонастраивающейся моделью (ГСМ) приведена на рис. 6.1.