Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 5

Задаются начальные условия

,   ,

 - единичная матрица, .

Выполняется  - шаговая  процедура

,     ,

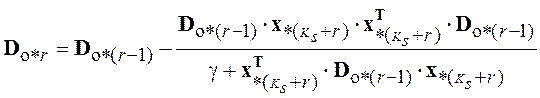, где

.

Приведенный алгоритм называется РМНК с взвешиванием в отличие от классического РМНК, где  . Параметр  служит для «забывания» старой информации, причем, чем меньше , тем больше информации «забывается». 

Корректирующими параметрами РМНК являются , , . Рекомендации по поводу выбора требуемого количества итераций  неизвестны.

4. СТРУКТУРНАЯ ИДЕНТИФИКАЦИЯ

 ЛИНЕЙНОГО СТАЦИОНАРНОГО ОБЪЕКТА

4.1. Общие положения

Математическиемодели в виде ДУ или ПФ являются наиболее общей формой уравнения связи между переменными состояния на входе и выходе линейного объекта при синтезе систем управления.

Ставится задача определения порядков  и  (структурная идентификация) и коэффициентов ,  (параметрическая идентификация) уравнения (1.1), описывающего линейный, непрерывный динамический (ЛНД) объект или порядков  и , и коэффициентов ,  уравнения (1.8), описывающего линейный дискретный динамический (ЛДД) объект. Уравнениям (1.1) и (1.8) соответствуют непрерывная ПФ (1.2) и дискретная ПФ (1.9).

В общем случае априорной информацией для решения поставленной задачи являются измеренные (как правило, с помехами) реализации входного  и выходного  сигналов объекта.

Иногда известна дополнительная информация о порядках ,  объекта идентификации, что существенно упрощает задачу определения математической модели.

4.2. Метод переходных функций

Метод переходных функций представляет собой простейший случай активной идентификации.

На вход идентифицируемого объекта подается ступенчатое воздействие. На выходе имеем переходную характеристику или, как ее иногда называют, кривую разгона. Полученная кривая аппроксимируется аналитическим выражением, например, вида

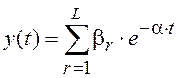, а далее, по аналитическим выражениям входного  и выходного  сигналов могут быть найдены их изображения по Лапласу в виде ПФ и затем ДУ .

Однако спектр сигнала типа ступенчатого воздействия близок к виду затухающей экспоненты и носит низкочастотный характер. В результате он является малоинформативным и точность определения характеристик объектов в области высоких частот с помощью метода переходных функций очень низка. Если же выходной сигнал  искажен случайными помехами, то качество идентификации еще более ухудшается.

Другие тестовые сигналы, которые удается реализовать, например, трапецеидальный, так же имеют спектры, которые носят низкочастотный характер.

Недостатки метода переходных функций частично парируются в, так называемых, частотных методах. Однако и они в настоящее время практически не используются.   

4.2. Структурная идентификация объекта посредством rl - процедуры

rl – процедура применяется при идентификации структуры и параметров ЛНД –  и  ЛДД – объектов. Суть ее рассмотрим на примере ЛНД – объекта.

На каждом  – том шаге итерационной процедуры, где , а  задается априори, параметр  последовательно принимает значения из диапазона , в результате чего получаем оценки модели (1.1) в виде  

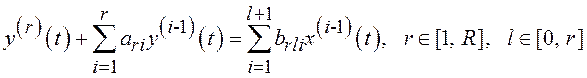.             (4.1)

При необходимости находятся и  – оценки ПФ

.

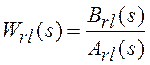Здесь же определяются и оценки коэффициентов полиномов  и , а также модельные сигналы

.                                 (4.2)

Далее вычисляются рассогласования

,                                (4.3)

а при необходимости и ряд других выборочных показателей, например, математические ожидания, дисперсии сигналов  и .

Оценки порядков  и  определяются в результате анализа совокупности функционалов . При этом вводится понятие состоятельности оценок, под которой понимается тот факт, что вероятность ошибки определения порядков  и  должна стремиться к 0 при .

Способы определения порядков  и могут быть объединены в три группы, которые базируются на:

1) исследовании ранговых критериев,

2) минимизации информационных критериев,

3) проверке статистических гипотез.

Дополнительная четвертая группа включает в себя другие, не вошедшие в первые три группы, подходы к определению структуры.

Ранговые критерии базируются на том, что на любом конечном или бесконечном интервале времени  совокупность  функций  представляют собой систему линейно независимых функций, поскольку