Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 8

Чем больше количество  формируемых уравнений (строк матрицы ), тем лучше обусловленность матрицы 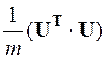 по причине более качественного усреднения высокочастотных помех при выполнении операции первой трансформации Гаусса.

Однако реализовать практически указанные выше рекомендации по выбору корректирующих параметров, как правило, не удается.

Если обозначить через ,  полосы пропускания формирующих фильтров, то параметр  может быть определен из условия

.                                                (5.10)

С другой стороны, для конкретного типа полосовых фильтров выполняется соотношение

,                                            (5.11)

где  - длительность ИХ  фильтра. Таким образом, чем уже полоса пропускания , тем больше длительность ИХ  и тем сложнее реализация фильтра.

Из (5.11) следует

.                                                    (5.12)

Подставляя (5.12) в (5.10) получаем

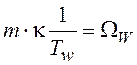, откуда

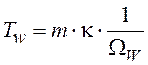.                                               (5.13)

В результате приходим к тому, что , а  .

Следует отметить, что идентифицируемые объекты, как правило, носят низкочастотный характер и, даже в случае   ,   разместить в диапазоне  АЧХ объекта  фильтров, с неперекрывающимися полосами пропускания , не удается.

5.2. Идентификация ЛДД – модели

ЛДД – модели описываются разностным уравнением

.

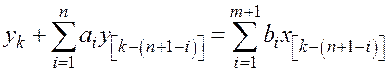С учетом помех  и , искажающих измеряемые сигналы на интервале  это уравнение будет иметь вид

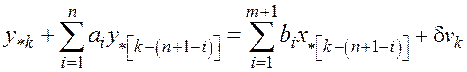,                    (5.14)

где 

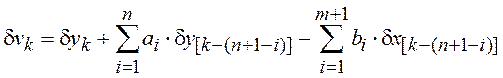                  (5.15)

обобщенная помеха.

Фиксируя уравнение (5.14) в точках   ,   где   ,  ,   ,   ,   - время переходного процесса или, что, то же самое, эффективная длительность ИХ,  раз получим систему линейных алгебраических уравнений

или

,                                               (5.16)

где

,

,

,

,

.

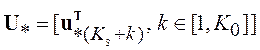Поскольку в общем случае , то система (5.16) приводится к виду

,                                    (5.17)

а искомое решение будем определять из системы

,                                            (5.18)

где

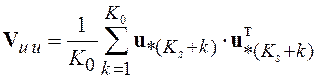 ,                                 (5.19)

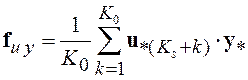 ,                                       (5.20)

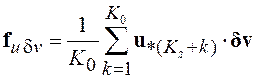.                                     (5.21)

Решение системы (5.18) ищется методом наименьших квадратов (МНК) из условия минимума функционала

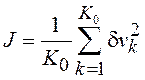, в результате чего МНК – оценка искомых параметров определяется из усеченной системы алгебраических уравнений

                                                (5.22)

в виде

.                                               (5.23)

Следует отметить, что МНК – оценки, найденные согласно (5.23) получаются смещенными относительно истинных параметров.

Ошибка идентификации

возникает из-за отбрасывания неизмеримого вектора  правой части системы и может быть уменьшена за счет компенсации влияния указанного вектора, что реализуется в, так называемом, прямом компенсационном МНК (ПКМНК).

Помимо компенсационного подхода возможны другие способы уменьшения ошибки идентификации. Для изложения этих способов воспользуемся аппаратом корреляционных функций.

Взаимная корреляционная функция между сигналами  и в идеальном случае выглядит как

.

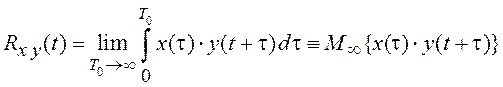Конечность длины интервала  и вычисление интеграла посредством квадратурной формулы позволяют определить лишь оценку

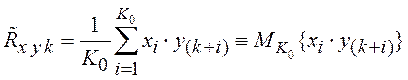.                        (5.24)

Если сравнить (5.24) с выражениями слагаемых системы (5.18), то очевидно, что элементы матрицы  и векторов  и  представляют собой отсчеты авто и взаимных корреляционных функций, что позволяет записать алгебраическую систему (5.18) в эквивалентном виде

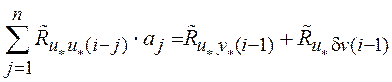.                         (5.25)

Из (5.25) следует - уменьшение ошибки идентификации будет иметь место, если:

1) оценка  будет стремиться к 0,

2) оценка  будет стремиться к истинной ,

3) оценка  будет стремиться к истинной .

Попытки реализации данных условий были сделаны в алгоритмах:

1) обобщенного МНК (ОМНК),

2) рекуррентного МНК (РМНК) и близкого к нему алгоритма Качмажа (АК),

3) метода инструментальной переменной (МИП), соответственно.

5.3. Прямой компенсационный МНК

Ставится задача скомпенсировать влияние неизмеримого вектора  системы (5.18) на ошибку идентификации. Для этой цели проведем анализ указанного вектора в предположении, что помеха , , а обобщенная помеха  не коррелирует с входным сигналом   .