Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 13

3) вычисляется вектор , который представляет собой решение - мерной неоднородной системы дифференциальных уравнений (8.8);

4) определяется оценка и вектора ;

5) вычисляется оценка , согласно выражению (8.6);

6) вычисляется функционал

,  , например, вида

;

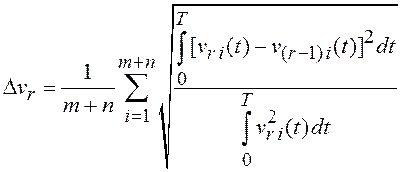7) производится сравнение вычисленного значения с наперед задаваемой величиной  и выносится соответствующее – при  осуществляется переход на следующий - ый шаг,  при  производится останов итерационной процедуры и принимается

,

,   ,

,           .

В заключении следует отметить, что оценка  начальных условий  (см. п.4) находится на основании первого уравнения системы (8.4), которое в развернутом виде выглядит как

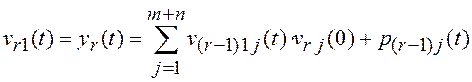
и представляет собой -ую оценку выходного сигнала объекта. Причем, поскольку  задаются априори (, ), то необходимо отыскать только  начальных условий , . Эту задачу можно решить из условия минимизации функционала

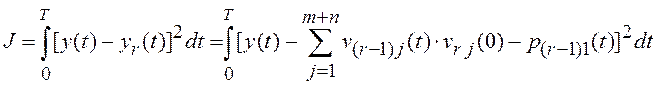
путем исследования его на экстремум, а именно

,      .

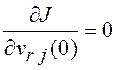В результате приходим к необходимости решения системы  линейных алгебраических уравнений

,   .

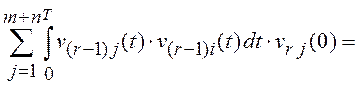
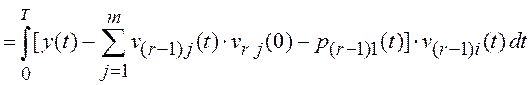Метод квазилинеаризации наряду с оцениванием параметров позволяет оценить при необходимости и вектор состояния нелинейного объекта, а в ряде случаев дополнительно и некоторые характеристики помех, что является достоинством метода.

Однако, в общем случае, сходимость метода квазилинеаризации не доказана. В результате оценивание расширенного вектора состояния существенно зависит от начальных условий. Исследования показывают, что если начальные условия выбраны достаточно близко, то алгоритм сходится. Кроме того, реализация метода предполагает существенные вычислительные затраты, связанные с формированием и решением обширных систем уравнений, что также негативно характеризует метод линеаризации.

Рассмотрим пример.

Объект описывается линейным (для простоты) дифференциальным уравнением

,

.

Эквивалентная система уравнений вида (8.1) с учетом обозначения   записывается в форме

,

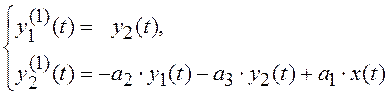а система (8.2) определяется выражением

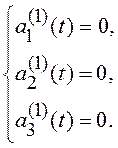
Вводя обозначения

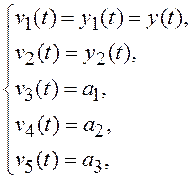
представим систему (8.3) в виде

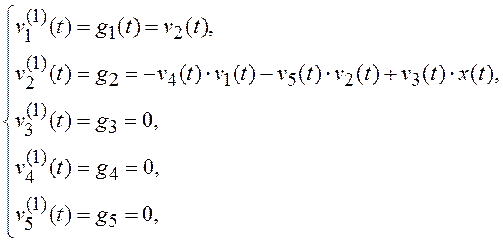
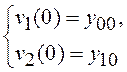
или

                             ,

                             .

Решение этой линейной системы согласно  (8.6) (система уравнений (8.4) нелинейная) будет

.

Для определения матрицы   необходимо решить систему (8.7), а это, в свою очередь, требует формирование матрицы  согласно (8.5)

=

,  ,  ,  ,  .

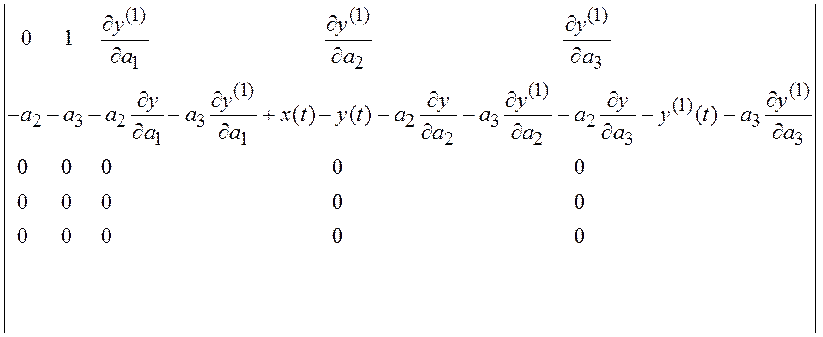
Уравнения чувствительности:

1)           при ;

2)         при ,

                                                                                ;

3)     при ,

                                                                                .

        

____________________________

 

_____________________________________________________________________

  ___________________________

.

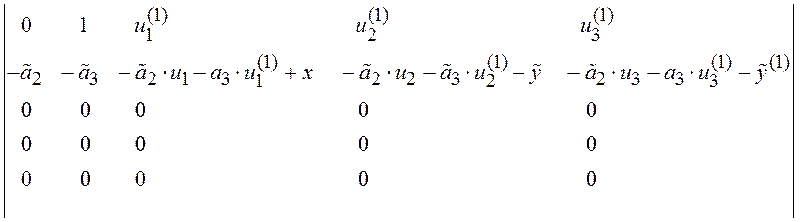
Это и есть система (8.7) в развернутом виде для рассматриваемого примера, решение которой

                                     .

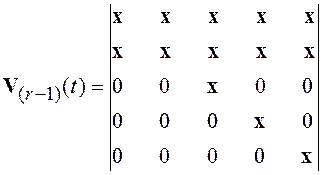9. ИДЕНТИФИКАЦИЯ НЕСТАЦИОНАРНЫХ ПАРАМЕТРОВ

(весь пункт переработан, с чем сравнивать?)

Пусть объект описывается уравнением

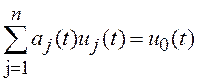.                                              (9.1)

Это может быть линейный объект 

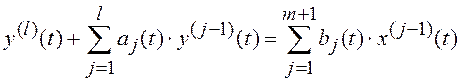, причем координаты

, , или нелинейный по координатам, но линейный по параметрам, например, объект, описываемый уравнением типа Риккати

.

Структура объекта (порядок ) известна.

Координаты  доступны измерению (обычно с помехами ) и представляют собой линейно независимые функции.

Предполагаются известными нижняя  и верхняя  граничные частоты  эффективной полосы спектра координат объекта и максимальная частота

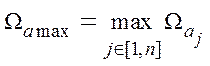
спектра идентифицируемых параметров, которую можно грубо оценить из физических законов функционирования идентифицируемого объекта.

Ставится задача текущей идентификации параметров

, .

Решение поставленной задачи базируется на формировании системы  уравнений, например, путем воздействия на уравнение (9.1) совокупности интегральных операторов Вольтера с ядрами  , .

В результате будем иметь

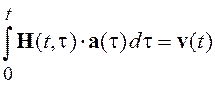,                                          (9.2)

где   ,

,

,   .

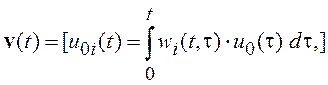На функции накладывается условие финитности, т.е.