Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 9

Представим вектор  в следующем виде

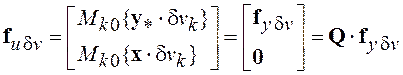.                         (5.25)

Соотношение (5.25) получено в предположении, что

, поскольку априори    и  ,  не коррелируют между собой. Матрица

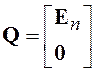
имеет мерность , а  - единичная матрица порядка .

На основании (5.18), (5.20) и (5.22) можно записать

.

В результате, если оценить вектор , то можно получить скомпенсированную оценку

.                                   (5.26)

Введем в рассмотрение расширенный вектор

, отличающийся от ранее используемого

и в результате определенных векторно-матричных преобразований получим

,                           (5.27)

где

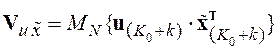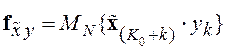,     ,     .     (5.28)

Таким образом, последовательность вычислительных этапов прямого компенсационного ПКМНК имеет следующий порядок.

1. Согласно выражениям (5.19), (5.20), (5.28) при  вычисляются оценки , , , .

2. Определяется МНК – оценка (5.23)

.

3. Оценивается неизмеримый вектор (5.27)

.

4. Вычисляется уточненная, скомпенсированная оценка (5.26)

.

Рис.17. График зависимости ошибки от N.

ПКМНК характеризуется новым корректирующим параметром - .

5.4. Обобщенный МНК

Ставится задача уменьшить (теоретически до нуля) уровень обобщенной помехи   за счет ее «выбеливания», которое заключается в том, что  представляется в виде реакции дискретного формирующего фильтра на белый шум . Это позволяет выразить обобщенную помеху в виде произведения белого шума на ПФ  фильтра, в результате чего взаимная корреляционная функция (неизмеримое слагаемое правой части системы уравнений) в выражении (5.25)        будет стремиться к нулю, поскольку белый шум не коррелирует ни с каким другим сигналом.

ПФ формирующего фильтра можно представить в виде авторегрессионной  (АР) модели

Рис. 5.4

и тогда

,     .

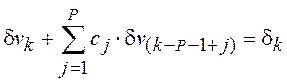Фиксируя значения параметра на интервале наблюдения можно сформировать систему линейных алгебраических уравнений, которая в векторно-матричном виде записывается как

,                                                 (5.29)

откуда

.                                                (5.30)

Подставляя (5.30) в алгебраическую систему (5.17) получим

.

В этом выражении слагаемое 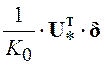 представляет собой взаимную корреляционную функцию между  и . В силу независимости

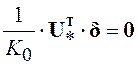
и тогда

.                                  (5.31)

Из (5.31) может быть найден искомый вектор  при условии, что будут известны  и .

Для оценивания матрицы   и вектора  представим (5.29) как

                                                (5.32) и преобразуем (5.32) к виду

, где

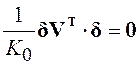
и в результате 

.                                        (5.33)

Из системы (5.33) можно определить вектор . Однако для этого предварительно оценивается обобщенная помеха  через МНК - оценку  (5.23).

Таким образом, вычислительная схема  ОМНК может быть представлена в следующем виде.

1. Выбирается порядок  формирующего фильтра из рекомендаций .

2. Запускается итерационная процедура, на каждом - ом шаге которой:

1) определяется оценка обобщенной помехи

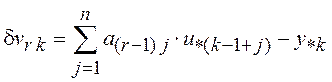,     , где в качестве начальных условий ,   используются грубые МНК – оценки, найденные обычным МНК;

2) из системы

вычисляется оценка вектора ;

3) находится оценка  вектора  путем решения системы

;

4) вычисляется норма

и выносится решение о прекращении или продолжении итерационной процедуры (в случае сходимости алгоритма имеем ).

Сходимость ОМНК  в значительной мере определяется порядком  формирующего фильтра, однако никаких конкретных рекомендаций по выбору этого параметра нет, в результате чего имеем проблему сходимости алгоритма, а  является корректирующим параметром ОМНК.

5.5. Рекуррентный МНК

С точки зрения реализации условия 2) уменьшения влияния неизмеримого вектора (5.21) системы (5.18) необходимо увеличивать количество формируемых уравнений. Такая возможность реально существует, поскольку алгебраическая система (5.18) формируется на интервале , а длина интервала  существенно меньше длины интервала наблюдения . Другими словами говоря, часть априорной информации (измеренные  и , ) не используется. Можно формировать системы уравнений последовательно на интервалах ,   и т. д., или в общем случае на , . Однако формирование  систем уравнений требует  обращений матриц сформированных систем, мерность которых увеличивается по мере возрастания , а это приводит к существенному росту вычислительных затрат. В результате была предложена рекуррентная процедура вычисления обратной матрицы, и, соответственно, РМНК параметрической идентификации.