Исследование системы на устойчивость двумя критериями. Синтез корректирующих устройств методом логарифмических частотных характеристик. Проверка результатов синтеза

3

МИНИСТЕРМТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КУРСОВАЯ

РАБОТА

Новосибирск 2007

                                                                                                                                                           4

Рисунок 1(структурная схема).

Расчетные данные:

1.1  Исследуем заданную систему на устойчивость двумя критериями.

а) Найдем передаточную функцию по управляющему воздействию разомкнутой системы

Введем обозначения:

Звенья W₁(p) и W₂(p) соединены посредством обратной связи. Найдем эквивалентное звено.

5

Приведем звено W₁₂(p) к произведению типовых звеньев.

Введемобозначения:

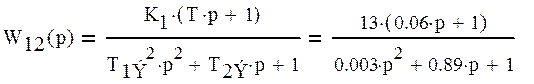
Звенья W₁₂(p), W₃(p), W₄(p) соединены последовательно. Перемножим эти звенья, чтобы получить эквивалентное звено разомкнутой системы по управляющему воздействию.

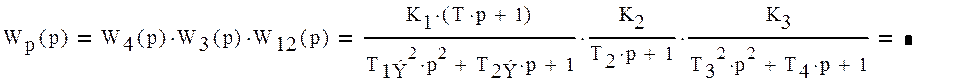
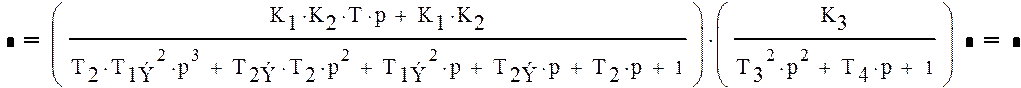
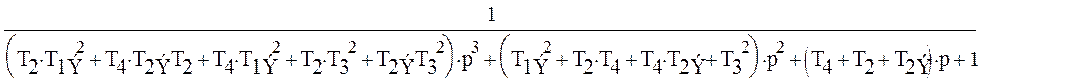
Подставляя значения, получим:

6

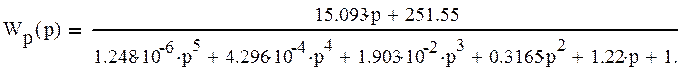
б) Найдем передаточную функцию по управляющему воздействию в замкнутом состоянии.

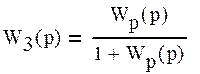
Для облегчения расчета сделаем некоторые упрощения.

Тогда передаточная функция замкнутой системы –W₃(p) равна:

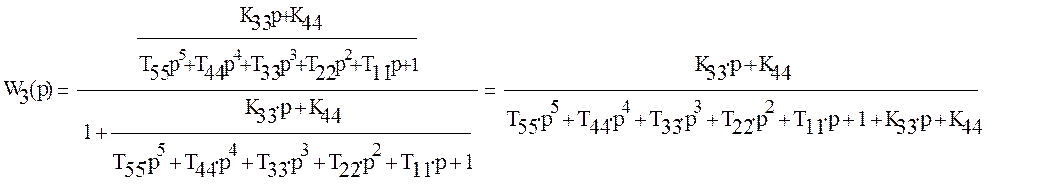
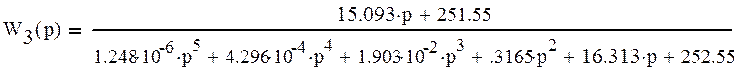
в) Найдем передаточную функцию ошибки Wg(p) по управляющему воздействию.

Схема замкнутой системы системы:

7

Рисунок 2(структурная схема)

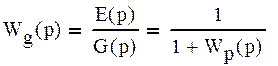
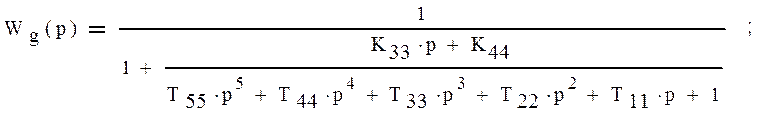
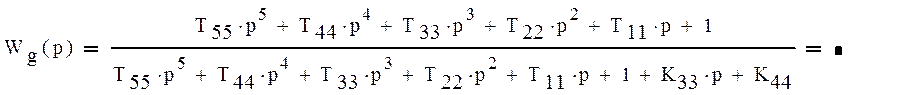
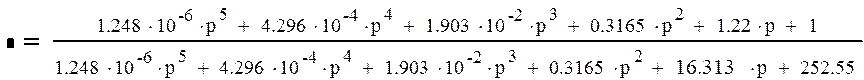
г) Характеристическое уравнение системы в разомкнутом состоянии.

Чтобы найти характеристическое уравнение системы в разомкнутом состоянии, нужно приравнять знаменатель разомкнутой передаточной функции к нулю.

д) Характеристическое уравнение системы в замкнутом состоянии.

Чтобы найти характеристическое уравнение системы в замкнутом состоянии, надо приравнять знаменатель передаточной функции  замкнутой системы по управляющему воздействию к 0.

8

е) Проверим устойчивость линейной САУ с помощью критерия Михайлова.

Критерий устойчивости Михайлова относится к частотным критериям. Этот критерий позволяет оценить устойчивость системы по виду годографа, получаемого из характеристического уравнения. Критерий Михайлова: чтобы система в замкнутом состоянии являлась устойчивой, необходимо и достаточно, чтобы вектор D(jω), описывающий своим концом кривую Михайлова при изменении частоты от  -∞ до +∞,вращаясь с действительной положительной оси против часовой стрелки, нигде не обращался в нуль, и проходил последовательно такое количество квадрантов, каков порядок характеристического уравнения.

Заменим p на jω.

Тогда получим:

С помощью этого уравнения можно построить годограф и судить об устойчивости системы.

Выделим мнимую Q(jω) и действительную P(jω) части вектора D(jω).

Определим значения P(w) и Q(w) для разных значений w. Сведем результаты в таблицу 1.1

9

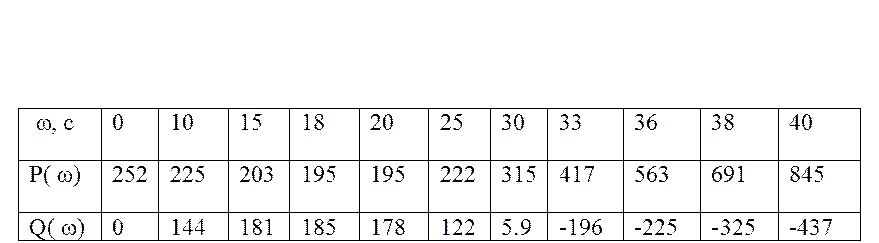
По табличным данным построим кривую Михайлова.(рисунок 3)

По кривой Михайлова видно, что условие устойчивости не выполняется, потому что кривая не проходит последовательно квадранты и обращается в ноль. Система не является устойчивой.

ж) Проверим устойчивость САУ с помощью критерия Найквиста.

Критерий Найквиста - графоаналитический критерий. Вывод об устойчивости замкнутой 

системы делается на основании ЛАЧХ или АФЧХ разомкнутой системы. Чаще используют ЛАЧХ, так как метод синтеза разработан для минимальнофазовых систем, у которых есть однозначная зависимость между ЛАЧХ и АФЧХ. Будем использовать обе характеристики, так как по одной нельзя определить запасов устойчивости. Критерий Найквиста помогает определить запас устойчивости и выяснить, как из неустойчивой САУ получить устойчивую. Формулировка критерия Найквиста в логарифмических координатах: если разомкнутая система устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы ЛФЧХ при изменении частоты от 0 до ∞ пересекала линию 180 градусов справа от частоты среза(точка пересечения ЛАЧХ с осью абсцисс).[1. стр 131]

Приведем систему к одноконтурной с последовательными соединениями типовых звеньев.

Рисунок4(структурная схема).

10

Разложим инерционное звено второго порядка W12(р) на два типовых апериодических звена. Оно инерционное, а не колебательное, потому что коэффициент демпфирования больше одного.

Найдем этот коэффициент.

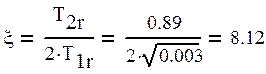
Раскладываем передаточную функцию.

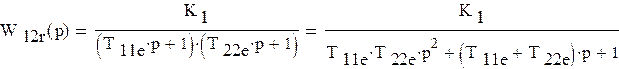
Введем некоторые обозначения:

Получим следующее:

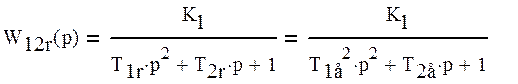
Найдем величины T_11e и T_22e. Составим систему из двух уравнений. Получим квадратное уравнение. Найдем его корни.

Корни этого уравнения имеют вид:

11

Этим корням соответствуют  следующие значения T_11e.

Разложим звено W_12r(p) на два

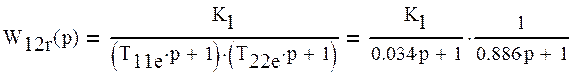
В итоге, после разложения этого звена, получили два апериодических звена.