Так как коэффициент демпфирования колебательного звена W4(p) меньше 1, то его не нужно раскладывать на 2 апериодических. Ошибка от аппроксимации должна быть меньше допустимой.
Итак, разложив структурную схему на ряд типовых звеньев получим передаточную функцию разомкнутой системы в виде:
![]()
Схема такой системы представлена ниже. Новые звенья обозначим по-новому.
Рисунок5(структурная схема).
В результате чего получили: 3 апериодических звена (W1(p),W2(p),W4(p)) одно форсирующее звено первого порядка (W3(p)),одно колебательное звено (W5(p)).
Для заданной САУ построим ЛАЧХ L(ω) в разомкнутом состоянии. По виду L(ω) можно судить об устойчивости замкнутой системы.
Найдем коэффициент усиления Кр.
![]()
Построение ЛАЧХ начинаем с выражения:
12
![]()
Найдем все частоты звеньев и логарифмы этих частот, соответствующие заданным постоянным времени.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛАЧХ состоит из пяти участков, разделенных логарифмом частоты среза того или иного участка.
1-ый участок имеет наклон -20дБ/дек (апериодическое звено);
2-ой участок имеет наклон -20дБ/дек - 20дБ/дек =-40дБ/дек (апериодическое звено);
3-ий участок имеет наклон -40дБ/дек+ 20дБ/дек = -20дБ/дек (форсирующее звено первого порядка);
4-ый участок имеет наклон -20дБ/дек - 40дБ/дек = -60дБ/дек (колебательное звено);
5-ый участок имеет наклон -60дБ/дек - 20дБ/дек = -80дБ/дек (апериодическое звено)
Чтобы построить АФЧХ нужно отложить по оси абсцисс логарифм частоты, которая
задается произвольно, а по оси ординат угол в градусах. Формулы для
определения углов и передаточные функции звеньев приведены ниже в таблице №1.
Таблица 1.
13
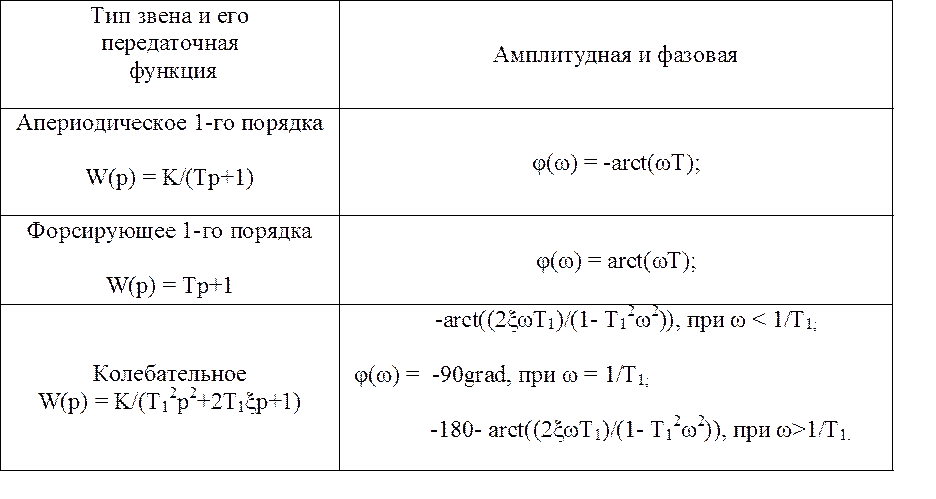
Выражение, по которому будет рассчитываться суммарное значение фазы, имеет вид:
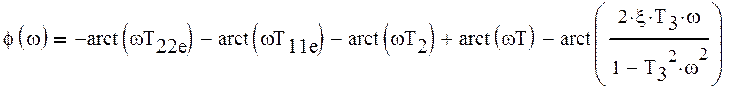
Подставляя в исходное выражение различные значения ω, построим АФЧХ и определим: устойчива ли система или нет.
Найдем значения φ, соответствующее заданным значением ω. Данные сведем в таблицу 2. АФЧХ и ЛАЧХ построим на миллиметровке(рисунок 6).
Таблица 2.
14
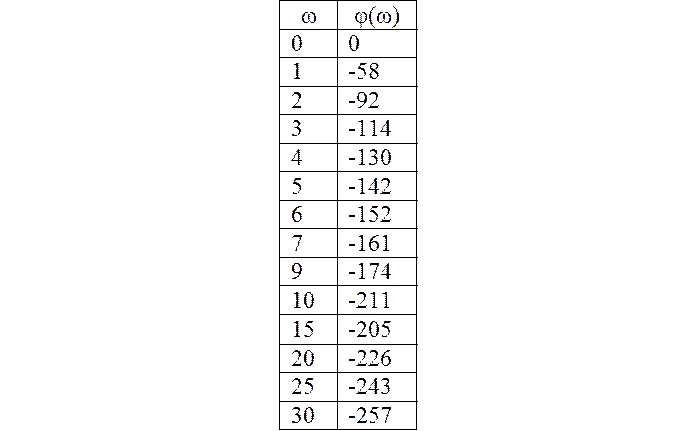
Построив АФЧХ и ЛФЧХ, убедились в том, что частота среза находится справа от точки пересечения АФЧХ с линией 180градусов. Отсюда следует, что система неустойчива. Оба метода определили систему, как неустойчивую. Следовательно, она не устойчива.
з) Чтобы окончательно убедиться в том, что система неустойчивая, воспользуемся критерием Гурвица.
Для определения устойчивости составляют определитель Гурвица по правилам:
1) По главной диагонали записывается коэффициент, начиная с а1 в порядке возрастания импульса.
2) Определитель заполняется по столбцам.
3) Вниз записывают коэффициент с убывающим индексом, вверх с возрастающим.
Недостающие коэффициенты заполняются нолями.
Знаменатель характеристического уравнения имеет вид:
![]()
Составляем определители Гурвица.
15
![]()
![]()
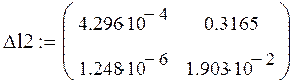
![]()
![]()
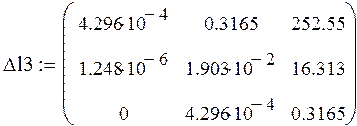
![]()
![]()
Δι3<0 - третий определитель меньше нуля. Из этого следует, что система не устойчивая.
1.2 Определение ошибки, заданной САУ в установившемся режиме.
Если на вход подать единичный сигнал Xвх = 1(t), то в установившемся режиме статическая ошибка (а она присутствует, так как в системе нет интегрирующего звена) будет определяться по формуле:
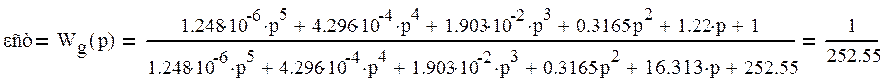
при p=0.
Система будет астатической по отношению к управляющему воздействию, если при стремлении управляющего воздействия к постоянной величине ошибка стремится к нулю и не зависит от величины управляющего воздействия.
Установившаяся ошибка определяется по выражению:
16
![]()
εc –скоростная ошибка.
![]() -статическая ошибка
-статическая ошибка
Установившаяся ошибка складывается из ошибки статической и скоростной, равной отношению скорости задания добротности к добротности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.