Новосибирский государственный технический университет
Кафедра электропривода и автоматизации промышленных установок
ОТЧЁТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ
Дисциплина: «Теория автоматического управления»
Работа № 3
«Исследование устойчивости линейных
систем автоматического управления»
Группа ЭМ-51 Бригада № 1
Состав бригады: 1. Солнцев А.
2. Тарасов В.
3. Похомов М.
Работа защищена:_________________________________
Преподаватель: Тюрин Максим Владимирович
2007 г.
1. ЦЕЛЬ РАБОТЫ
Используя метод структурного моделирования, исследовать заданную систему автоматического управления на устойчивость. Установить влияние параметров системы на ее устойчивость и определить их граничные (критические) значения.
2. ПРОГРАММА ПОДГОТОВКИ К ЛАБОРАТОРНОЙ РАБОТЕ
2.1
Одним из алгебраических критериев определить устойчивость заданной САУ и
рассчитать граничные значения коэффициента передачи системы kи постоянной времени ![]() .
.
Структурная схема имеет вид:

Значения параметров:
|
Номер варианта |
Численные значения параметров |
|||
|
1 |
|
8 |
|
2 |
|
|
7 |
|
4 |
|
|
|
2 |
|
0.1 |
|
Проверка САУ на устойчивость по методу Гурвица
1) Передаточная функция САУ в замкнутом состоянии:
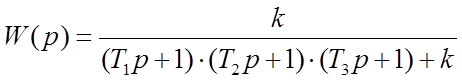
где ![]()
Формулировка критерия Гурвица:
Для
устойчивости САУ необходимо и достаточно, чтобы при ![]() все
диагональные миноры определителя Гурвица были положительными.
все
диагональные миноры определителя Гурвица были положительными.
2) Найдем характеристическое уравнение заданной системы
Приравняем к нулю знаменатель передаточной функции:
![]()
Раскроем скобки:
![]()
Обозначим коэффициенты уравнения и найдем их значения:
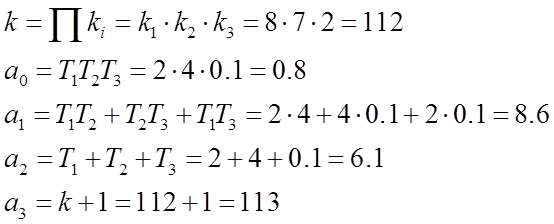
Характеристическое уравнение замкнутой примет вид:
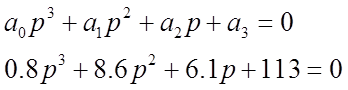
3) Запишем определитель Гурвица:
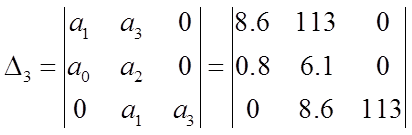
Условия устойчивости:
![]()
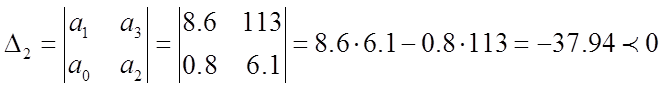
Т.к.
![]() , то делаем вывод, что заданная система
неустойчивая.
, то делаем вывод, что заданная система
неустойчивая.
4) Определим влияние параметров системы на ее устойчивость.
Рассчитаем
граничные значения параметров системы ![]() и
и ![]() :
:
Для
этого запишем условие нахождения заданной САУ на границе устойчивости ![]()
Найдем
![]()
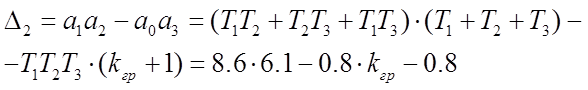
Выразим искомое значение:
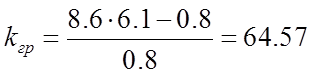
Найдем
![]()
Возьмем
в качестве неизвестного параметр ![]() и запишем условие
границы устойчивости:
и запишем условие
границы устойчивости:
![]()
Раскроем скобки и решим получившееся квадратное уравнение
![]()
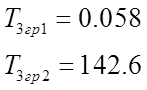
(в
лабораторной работе мы использовали ![]() )
)
Для определения влияния этого параметра на устойчивость заданной САУ необходимо дополнительно исследовать устойчивость системы при уменьшении и увеличении этого параметра относительно его граничных значений.
Проверка САУ на устойчивость по критерию Найквиста
Формулировка критерия устойчивости Найквиста: если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении ω от нуля до ∞, не охватывала точку с координатами (-1; i0).
АФЧХ разомкнутой системы имеет вид:
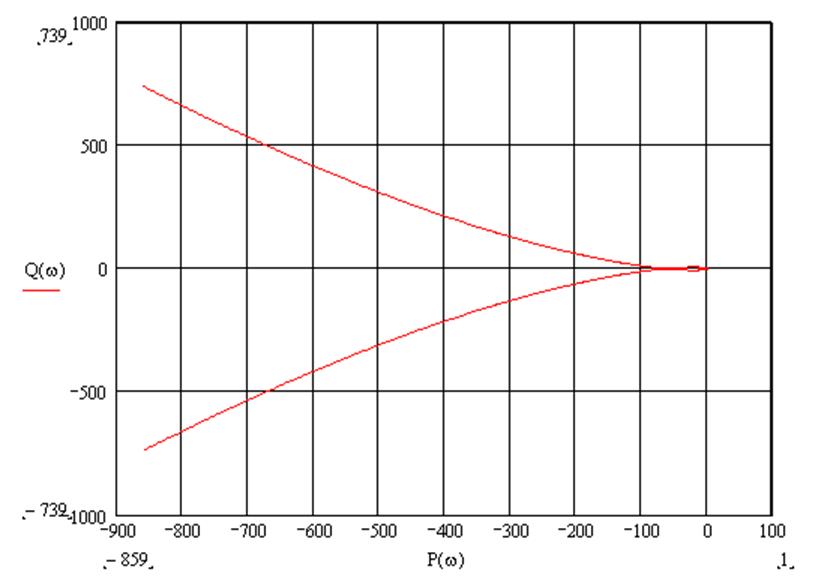
По виду зависимости можно сказать. Что разомкнутая система неустойчивая, а следовательно и замкнутая тоже.
3. Опытная проверка результатов.
3.1) Для заданной САУ снять график переходной функции и по ее виду определить устойчивость системы.
Структурная схема с заданными параметрами имеет вид (в программе MATCAD):

Переходная характеристика заданной САУ имеет следующий вид:
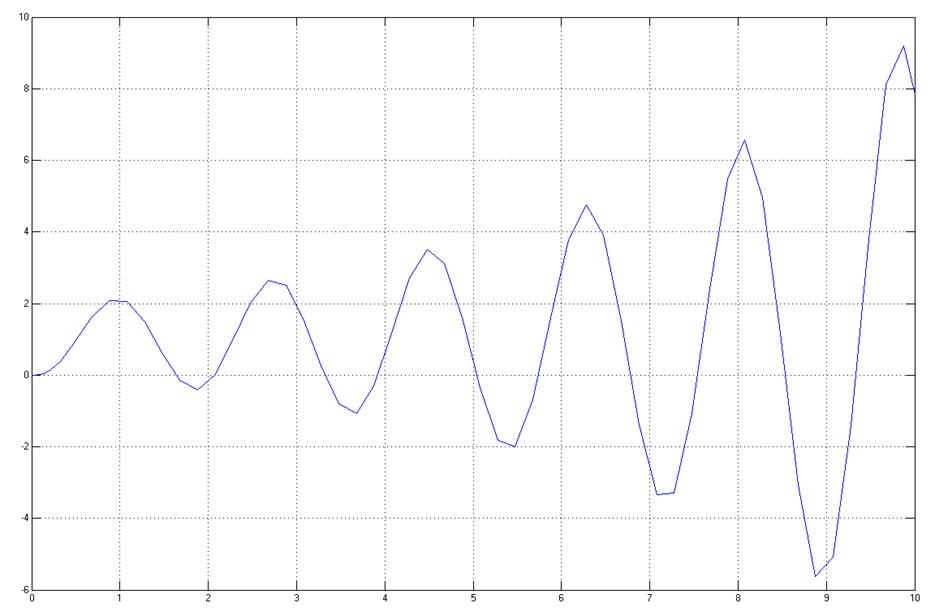
3.2) Исследование влияния коэффициента передачи на устойчивость системы: определить (опытным путем) граничное значение коэффициента передачи и найти области устойчивости (неустойчивости). Снять графики переходных функций устойчивого и неустойчивого режимов работы и границы устойчивости.
![]()
Изменим
значение одного из заданных коэффициентов: пусть ![]() , тогда
, тогда ![]() и переходная характеристика будет иметь
вид:
и переходная характеристика будет иметь
вид:
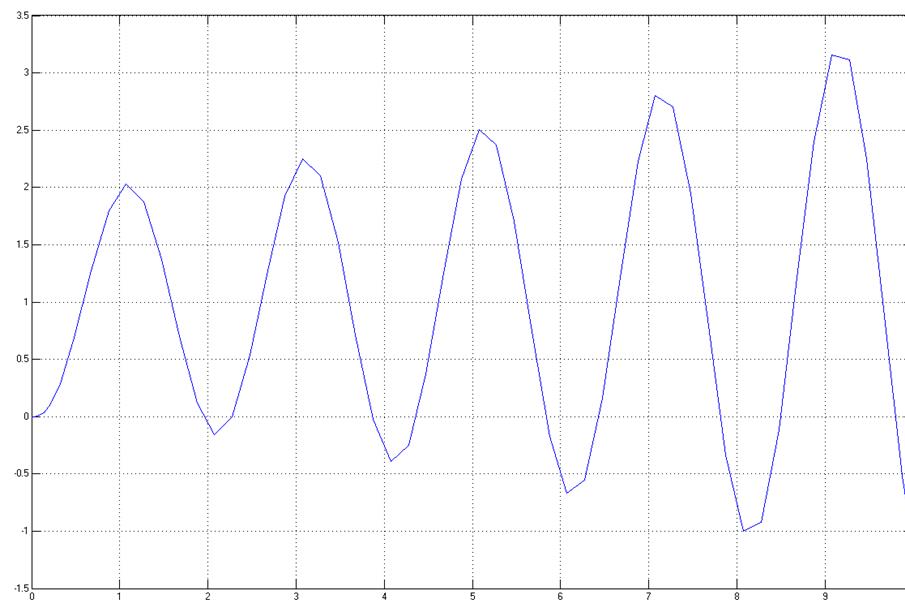
Пусть
![]() , тогда
, тогда ![]() и
переходная характеристика будет иметь следующий вид:
и
переходная характеристика будет иметь следующий вид:
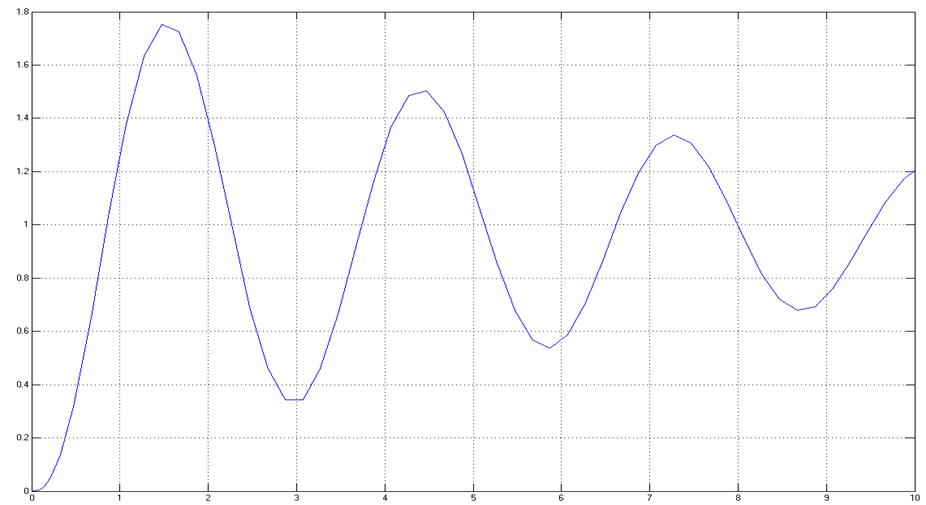
Подбирая
К таким же образом, находим, что ![]() равно 1.15, при этом
граничный коэффициент передачи замкнутой системы равен:
равно 1.15, при этом
граничный коэффициент передачи замкнутой системы равен:
![]()
При таком коэффициенте передачи замкнутой системы переходная характеристика имеет вид:
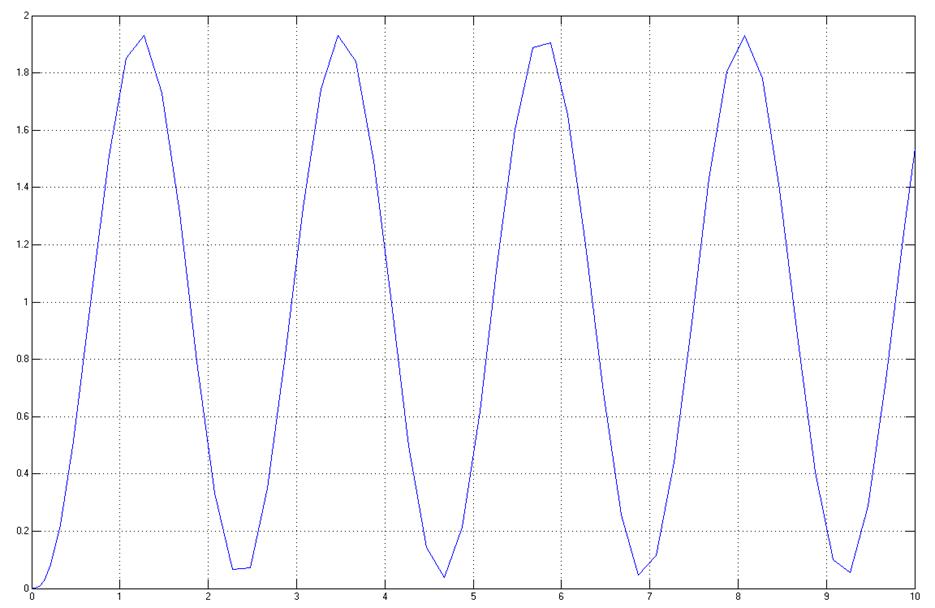
Делаем
вывод, что САУ находится на границе устойчивости и область устойчивости ![]() .
.
3.3)
Выставить на модели заданное значение коэффициента передачи и исследовать
влияние постоянной времени ![]() на устойчивость
системы: определить граничные значения постоянной времени
на устойчивость
системы: определить граничные значения постоянной времени ![]() и найти области устойчивости
(неустойчивости). Снять графики переходных функций устойчивого и неустойчивого
режимов работы и границ устойчивости.
и найти области устойчивости
(неустойчивости). Снять графики переходных функций устойчивого и неустойчивого
режимов работы и границ устойчивости.
При
заданном значении постоянной времени ![]() переходная
характеристика имеет вид:
переходная
характеристика имеет вид:
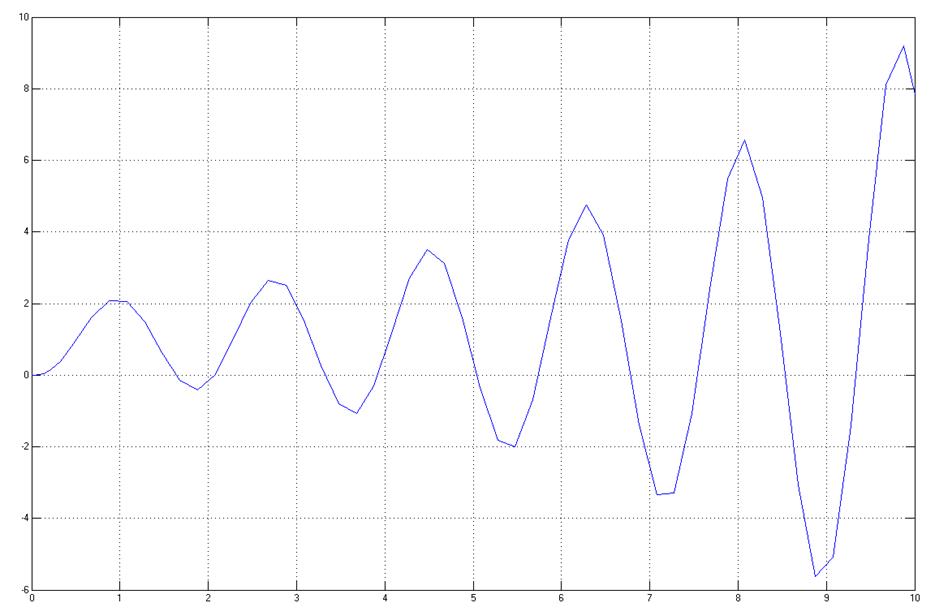
Изменяем
значение ![]() в большую и в меньшую стороны и снимаем
переходные характеристики:
в большую и в меньшую стороны и снимаем
переходные характеристики:
Пусть
![]() равно 0.15, тогда
равно 0.15, тогда
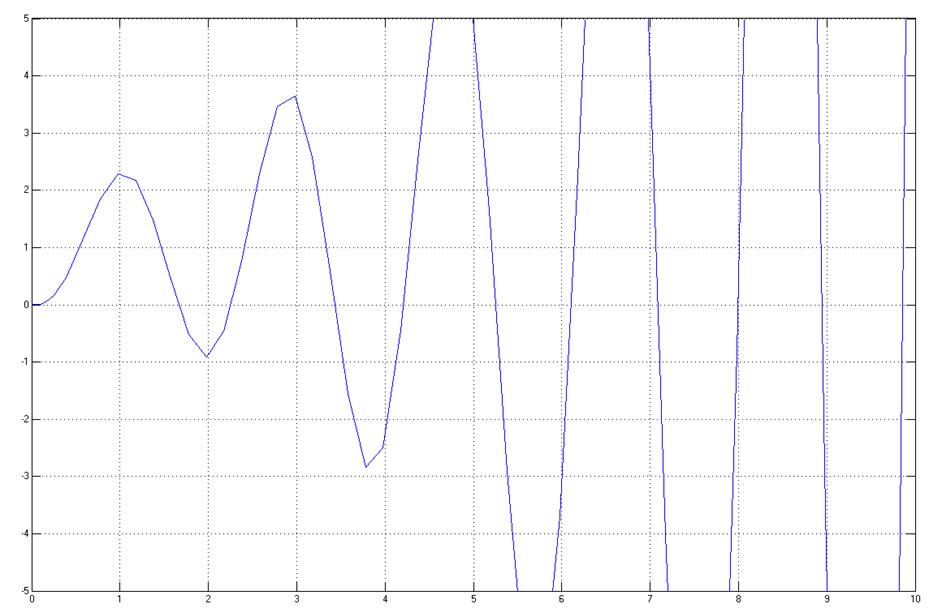
Система неустойчивая.
Пусть
значение ![]() равно 0.055, тогда
равно 0.055, тогда
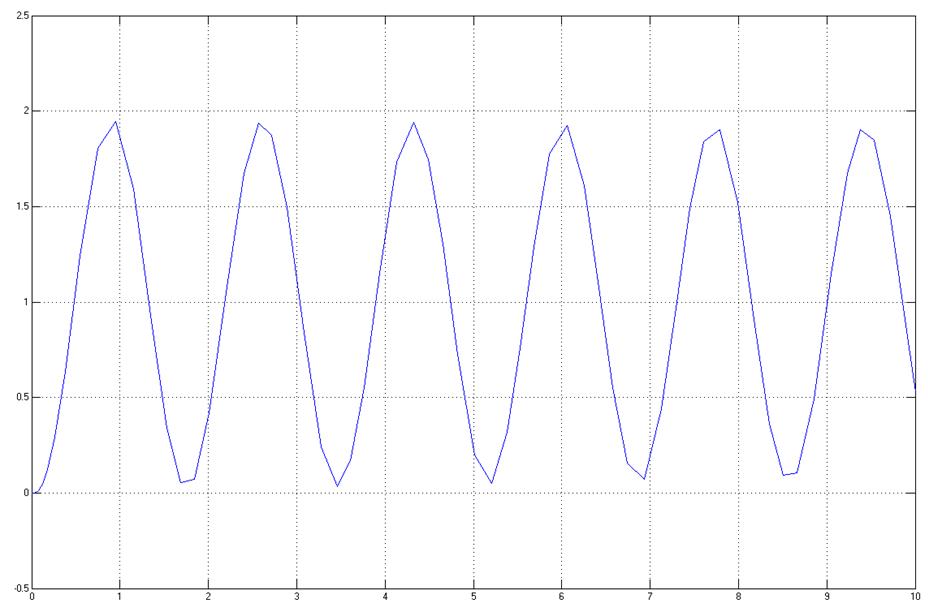
система
находится на границе устойчивости, следовательно ![]() равно
0.057
равно
0.057
Если
взять значение Т меньше ![]() , то переходная
характеристика будет устойчивая, это значит, что область устойчивости
, то переходная
характеристика будет устойчивая, это значит, что область устойчивости ![]() . Пусть Т=0.03.
. Пусть Т=0.03.
График переходной характеристики при этом будет иметь вид:
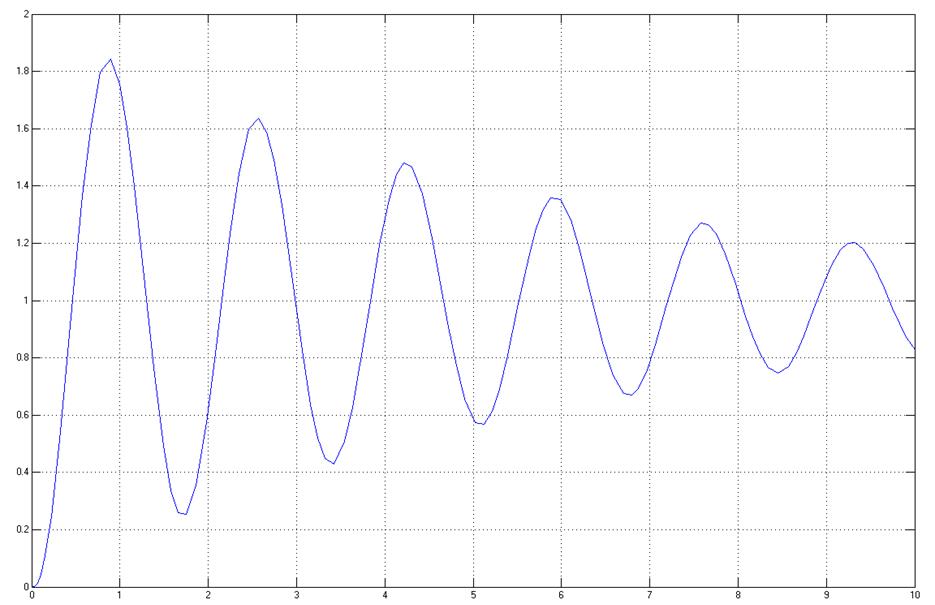
Переходная характеристика устойчивая, значит область устойчивости указана верно.
Нужно
отметить, что существует еще одна область устойчивости полученная теоретически,
она запишется так: ![]() .
.
3.4)Снять частотные характеристики А(ω) и φ(ω) для заданной САУ в разомкнутом состоянии и по ним проверить устойчивость системы по критерию Найквиста. При снятии частотных характеристик в качестве обязательных взять частоты сопряжения звеньев.
Поставим на вход разомкнутой системы источник гармонического сигнала, при этом структурная схема примет вид:
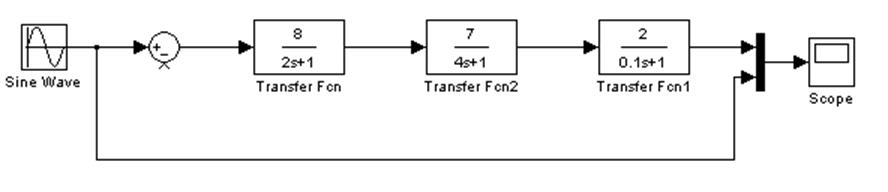
Изменяя частоту источника ω снимаем зависимости А(ω) и φ(ω), данные заносим в таблицу:
Частоты сопряжения звеньев входящих в заданную САУ равны
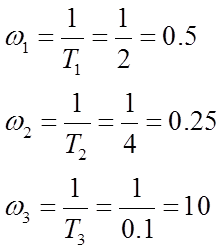
|
ω |
0.1 |
0.2 |
0.25 |
0.3 |
0.4 |
0.5 |
0.6 |
1 |
8 |
9 |
10 |
11 |
15 |
|
А(ω) |
103 |
82 |
71 |
61 |
45 |
36 |
27.5 |
12.3 |
0.2 |
0.15 |
0.13 |
0.1 |
0.05 |
|
φ(ω) |
51 |
43.6 |
60 |
85.7 |
104.5 |
100.8 |
120 |
42,5 |
270 |
25.7 |
28 |
44.2 |
25.1 |
|
Твх |
60 |
33 |
30 |
21 |
15.5 |
12.5 |
10.5 |
22 |
0.8 |
0.7 |
0.63 |
0.57 |
0.43 |
|
Твых |
68.5 |
37 |
25 |
26 |
20 |
16 |
14 |
24.6 |
1.4 |
0.75 |
0.6 |
0.5 |
0.4 |
|
tр |
8.5 |
4 |
5 |
5.3 |
4.5 |
3.5 |
3.5 |
2.6 |
0.6 |
0.05 |
0.05 |
0.07 |
0.03 |
Поданным таблицы в программе MATLAB строим графики.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.