1. Управляемая и наблюдаемая сопровождающие формы
УПРАВЛЯЕМАЯ И НАБЛЮДАЕМАЯ СОПРОВОЖДАЮЩИЕ ФОРМЫ
В описании систем в уравнениях состояния часто используется сопровождающая форма (companionform):
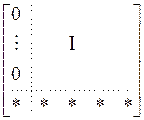 .
.
Рассмотрим скалярную систему порядка n:
![]() .
.
Пусть она будет управляемой (controllable) (говорят: пара матриц {А, b} управляема), т.е. матрица управляемости (controllabilitymatrix) θ = [b, Ab, …, An-1b] имеет ранг n. Обозначим последнюю строку матрицы θ-1 через q1 и введем матрицу
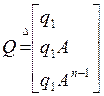 .
.
Оказывается,
что если перейти к новой переменной ![]() :
:
![]() ,
,
матрица ![]() будет представлена в сопровождающей форме:
будет представлена в сопровождающей форме:
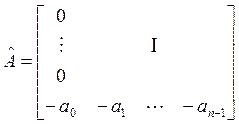 ,
, 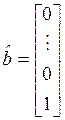 .
.
Представление матриц А, b в таком виде называется управляемой сопровождающей формой (controllablecompanionform).
Перейдем к управляемой многоканальной системе:
![]() ,
,
где
матрица В полного
ранга и вектор u имеет
размерность m(m![]() n).
n).
Из матрицы управляемости
θ = [B, AB, …, An-1B]
выделим ![]() линейно независимых столбцов. Полученную
матрицу размера n*
линейно независимых столбцов. Полученную
матрицу размера n* ![]() назовем
назовем ![]() . Из
управляемости следует n=
. Из
управляемости следует n=![]() , т.е. из |
, т.е. из |![]() | ≠ 0.
| ≠ 0.
Построим
матрицу L размером n* ![]() из
из ![]() перестановкой столбцов
перестановкой столбцов
L = ![]() .
.
![]()
![]()
![]()
Числа ![]() ,
, ![]() , называют индексами управляемости (controllabilityindices), а число
, называют индексами управляемости (controllabilityindices), а число ![]() -
индексом управляемости.
-
индексом управляемости.
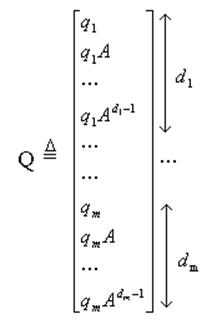 |
Перейдем к новым координатам ![]() Qx. В уравнении пространства состяний
Qx. В уравнении пространства состяний ![]() матрицы имеют конечный вид:
матрицы имеют конечный вид:
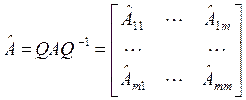 ,
, 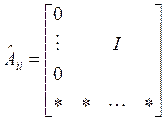 ,
,
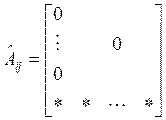 ,
, 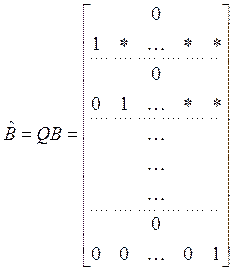
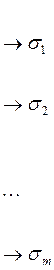 .
.
(i ≠ j) 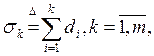
Канонический вид матриц ![]() называется
сопровождающей формой (controllablecompanionform).
называется
сопровождающей формой (controllablecompanionform).
Пример. Для матриц
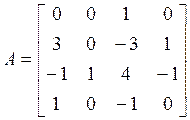 и
и 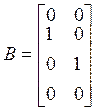
найти сопровождающую форму. Прежде всего, проверяем управляемость системы, для чего находим произведение матриц АВ, А2В:
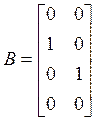 ,
, 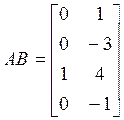 ,
, 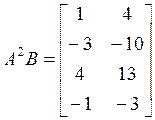 .
.
![]()
![]()
![]()
![]()
четыре
отмеченных столбца [b1, b2, Ab2, A2b2] линейно независимы, следовательно,
система управляема. Матрица L = ![]() = [b1, b2, Ab2,
A2b2] (т.е. d1 = 1, d2 = 3, σ1 = d1 = 1, σ2 = d1 + d2 = n =
4) такова:
= [b1, b2, Ab2,
A2b2] (т.е. d1 = 1, d2 = 3, σ1 = d1 = 1, σ2 = d1 + d2 = n =
4) такова:
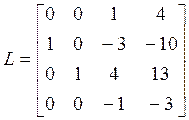 .
.
Находим матрицу L-1 и берем из нее строку q1 ( σ1 = 1) и q2 ( σ2 = 4)
q1 = [1 1 0 -2], q2 = [1 0 0 1]
и строим матрицу Q и ее обратную Q-1:
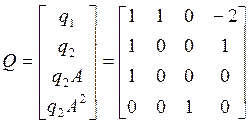 ,
, 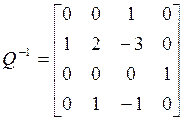 .
.
Вычисления заканчиваем поиском матриц
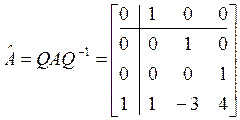 ,
, 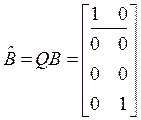 ■
■
Рассмотрим случай, когда система неуправляема, т.е.
ранг матрицы управляемости меньше n: rank(θ)= ![]() . Здесь поступаем,
как выше, а именно, берем первые
. Здесь поступаем,
как выше, а именно, берем первые ![]() линейно независимых столбцов θ с номером последней строки
линейно независимых столбцов θ с номером последней строки ![]() . Эти
. Эти ![]() столбцов образуют подпространство
столбцов образуют подпространство ![]() , Берем ортогональное дополнение (orthogonalcomplement)
, Берем ортогональное дополнение (orthogonalcomplement) ![]() размерности
размерности
![]() с базисом β1, β2, … βq
с базисом β1, β2, … βq![]() и расширим пространство состояний:
и расширим пространство состояний:
![]()
![]()
![]()
![]() ,
, ![]() .
.
![]()
![]()
К этой системе применим процедуру поиска матрицы Q, но обозначим ее Qe. Формулы преобразования:
![]()
![]()
![]()
![]()
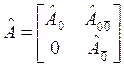 ,
, 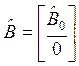 .
.
Система в новом базисе расщеплена две подсистемы:
![]() -
управляемая часть,
-
управляемая часть,
![]() -
полностью неуправляемая часть.
-
полностью неуправляемая часть.
Аналогично можно найти наблюдаемую сопровождающую форму для системы
![]()
![]()
где С – матрица полного ранга. Пусть указанная система наблюдаема (говорят еще: «пара {A, C} наблюдаема»). Можно перейти к дуальной задаче и рассматривать управляемую систему
![]()
которая преобразованием Q (см. приведение к канонической управляемой форме) приводится к каноническому виду
![]()
![]()
![]() .
.
Далее возвращаемся к исходной системе:
![]()
![]()
![]()
![]()
Преобразование
![]() сводит исходную систему к наблюдаемой
канонической форме (observablecompanionform):
сводит исходную систему к наблюдаемой
канонической форме (observablecompanionform):
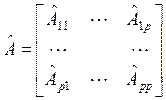 ,
, 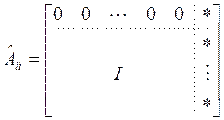 ,
,
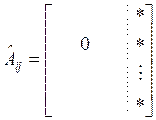 ,
, 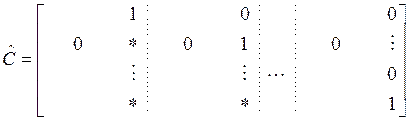 .
.
Матрица ![]() имеет p ненулевых столбцов с номерами
имеет p ненулевых столбцов с номерами 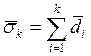 (
(![]() ). Числа
). Числа ![]() называют
индексами наблюдаемости (observabilityindices), а число
называют
индексами наблюдаемости (observabilityindices), а число ![]() - индексом
наблюдаемости. Таким образом, для определения
- индексом
наблюдаемости. Таким образом, для определения ![]() нужно
знать p индексов наблюдаемости
нужно
знать p индексов наблюдаемости ![]() и вычислить матрицы по формулам
и вычислить матрицы по формулам ![]() ,
, ![]() .
.
Пример. Найдем наблюдаемую сопровождающую форму для
системы: ![]() ,
, ![]() при
при
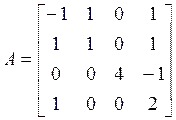 ,
, 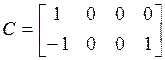 .
.
Перейдем к сопряженной системе ![]() , где
, где ![]() ,
, ![]() и
найдем сопровождающую управляемую форму для пары {
и
найдем сопровождающую управляемую форму для пары {![]() }. В данном случае матрица
управляемости
}. В данном случае матрица
управляемости
![]()
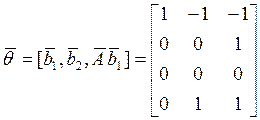
имеет
ранг, меньший 4, следовательно, нужно расширить матрицу ![]() .
Для этого возьмем линейно независимый r
.
Для этого возьмем линейно независимый r ![]() вектор
вектор ![]() . В
этом случае {A, Be} полностью управляема и
. В
этом случае {A, Be} полностью управляема и
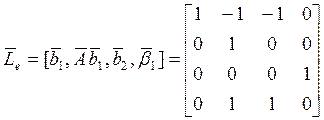 ,
,
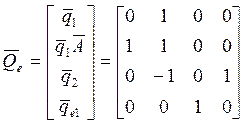 ,
, 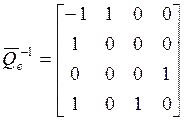 ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
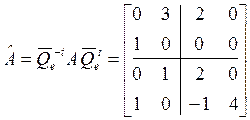 ,
, 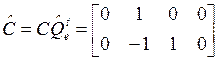 ■
■
Наблюдаемаячасть
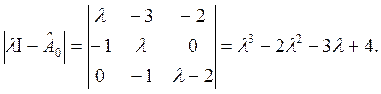
Ненаблюдаемой части соответствует λ=4.
2. Структурная теорема
Рассмотрим вопрос перехода от пространственного описания управляемой системы {A, B, C, E}, где В – полного ранга, к передаточной функции. Из управляемости следует существование невырожденного преобразования Q к новым переменным, где система представлена в управляемой сопровождающей форме:
![]() .
.
Из матрицы ![]() выделим матрицу
выделим матрицу ![]() размером
m*n (m упорядоченных строк с номерами
размером
m*n (m упорядоченных строк с номерами ![]() из
из ![]() ), а из матрицы
), а из матрицы ![]() выделим
матрицу
выделим
матрицу ![]() размерами m*n (m
упорядоченных строк с номерами
размерами m*n (m
упорядоченных строк с номерами ![]() из
из ![]() ). Введем еще матрицу S(s), которая
совместно с
). Введем еще матрицу S(s), которая
совместно с ![]() приведена ниже:
приведена ниже:
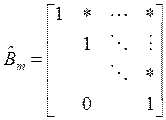 ,
, 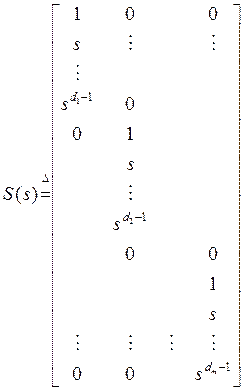 .
.
Теорема (структурная теорема). Если пространственное представление {A, B, C, E} соответствует управляемой системе с В полного ранга при m≤n, то ее передаточная функция T(s) вида C(sI-A)-1B+E может быть выражена так:
![]() , где
, где
 ■
■
Таким образом, представили объект в виде «числителя» и «знаменателя» T(s)=R(s)P-1(s) (правое полиномиальное разложение), где
![]() ,
, ![]() , и получили формулу для вывода
матричной передаточной функции
, и получили формулу для вывода
матричной передаточной функции
![]() .
.
Свойства этих матриц следующие:
1) матрица P(s) полиномиальная столбцово правильная;
2) степень каждого столбца Rj(s)матрицы P(s).
Пример. Для системы, заданной в пространстве состояний
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.