Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 5

где

,

.

 - коэффициентная матрица при производных ,

 - коэффициентная матрица при векторе состояний ,

 - матрица коэффициентов при производных .

Последние  строк  образуют транспонированную матрицу наблюдаемости. В обычно используемой форме строки присутствуют в противоположном порядке. Это множество уравнений позволяет получить, по крайней мере, одно уравнение, которое связывает сумму взвешенных производных выхода  с суммой взвешенных производных входа . Это может быть выполнено применением процедуры исключения Гаусса к .

Удобно выполнять процедуру приведения Гаусса в форме «коэффициентной генерирующей матрицы»

размерами . Она состоит в приведении к верхнетреугольному виду, начиная с элемента (1, 1) матрицы . В исходной матрице  матрица  берется вида единичной.

Случай 1: Система полностью наблюдаемая

Так как  имеет строк больше чем столбцов, это гарантирует наличие нулевых строк внизу результирующей матрицы при приведении к верхнетреугольному виду . В случае, когда имеем единственную нулевую строку внизу, эта строка обеспечивает желаемое отношение между выходной переменной и входной переменной, и коэффициенты при производных   есть коэффициенты характеристического полинома по выходу и также матрицы . Примеры 1 и 2 иллюстрируют этот случай.

Случай 2: Система не полностью наблюдаема по выходу

Если система не наблюдаема по выходу, тогда более одной нулевой строки будет получено в результате процедуры исключения Гаусса (число нулевых строк будет , где  степень вырождения матрицы наблюдаемости). В данном случае имеем  совершенно равноправных случаев выбора для представления передаточной функции. Эту свободу можно использовать для исключения общих членов в этих представлениях, сравнивая  уравнений. Привлекательна процедура исключения старших производных выхода, позволяющая генерировать передаточную функцию по выходу с наименьшей возможной степенью. Это легко выполнить, продолжая процедуру приведения к верхнетреугольному виду над частью  из  с использованием перестановки столбцов.

Характеристический полином А

Характеристический полином матрицы состояний  может быть определен с использованием указанной процедуры, для чего следует сформировать фиктивный выход, при котором система была полностью наблюдаема, например, взять

.

В этом случае следует рассматривать лишь сокращенную коэффициентную генерирующую матрицу

.

Только существование нулевого собственного значения  может привести к появлению более чем одной нулевой строки . Однако дальнейшие преобразования над  с целью приведения к верхнему треугольному виду невозможны.

Пример 1. Рассмотрим полностью наблюдаемую систему по входу-выходу:

,  .

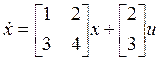Коэффициентная генерирующая матрица

становится равной

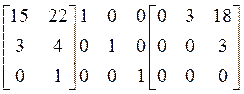
и результирующая верхнетреугольная форма такова:

.

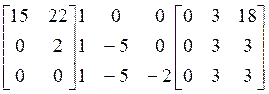Как мы можем увидеть из нижней строчки, дифференциальное уравнение «вход-выход» равно

.

Нормализацию ведущего элемента проводить нет необходимости, так как здесь использована целочисленная арифметика ■

Пример 2. Рассмотрим не полностью наблюдаемую по выходу систему

,  .

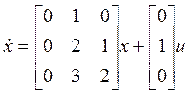С использованием этих данных находим матрицу :

.

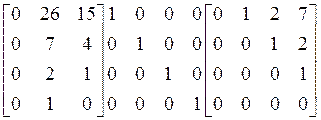Приведем левый блок к верхнетреугольному виду

.

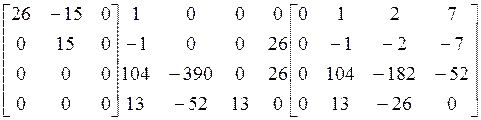Нормализация ведущих элементов также не производилась, что вызвано использованием целочисленной арифметики.

Каждая из двух нижних строк представляет равноправные дифференциальные уравнения относительно  и :

,

.

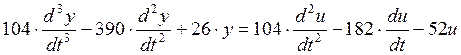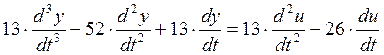Однако наличие двух линейно независимых уравнений позволяет исключать любые члены с  и  и их производными, имеющимися в этих уравнениях. Обоснованным критерием является понижение порядка дифференциального уравнения настолько, насколько это возможно. Это может быть достигнуто продолжением процедуры приведения к верхнетреугольному виду над , в результате чего результирующие нижние две строки будут

.

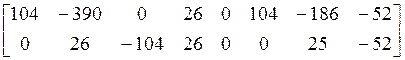Преобразование нижней строки приводит к желаемому минимальному порядку уравнения относительно  и

  ■

Пример 3. Вычислим характеристический полином матрицы, приведенной в предыдущем примере. В соответствии с рекомендацией организуем выход в виде

, в предположении, что сформированная система будет полностью наблюдаемой. Мы получим