Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 12

Вначале выберем какой-нибудь элемент в первой строке матрицы . С целью достижения наименьшей вычислительной ошибки обычно выбирают наибольший. Затем, используя элементарные строчные операции, полагаем (делаем) остальные элементы этого столбца равными нулю. Те же манипуляции выполняем и для второй строки  и т.д. Наконец, матрица  преобразована к верхнетреугольному виду ( с учетом перестановок столбцов) последовательностью строчных операций. С целью решения (1) посредством использования строчного поискового алгоритма (row searching algorithm) запишем уравнение

в виде

                                               (4)

Отметим, что используя строчный поисковый алгоритм получим

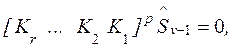                                                                     (5)

где К₁ , К₂ ,  …  , К_r  – нижнетреугольные константные матрицы с единицами на диагоналях. Они представляют последовательность элементарных строчных операций. Матрица  обозначает последние p строк произведения .

Таким образом, все коэффициенты L(s) и M(s) могут быть найдены из матрицы , т.е. из строчного поискового алгоритма.

Следующая лемма касается порядка матриц L(s) и M(s), полученных по указанному алгоритму.

Л е м м а 2. При заданных ,  и  порядки матриц L(s) и M(s), полученных поисковым строчным алгоритмом, наименьшие.

Д о к а з а т е л ь с т в о. Уравнение (4) показывает, что если будут использованы верхние строчки из  для получения уравнения, тогда будет уверенность, что L(s) и M(s) будут иметь наименьшие порядки. Отметим, что коэффициенты L(s) и M(s) зависят от тех же коэффициентов , что и D(s)  и N(s), т.е. строки  от строк . Так как  (4) и (5) могут быть решены строка за строкой, рассмотрим, во-первых, первую строку  . В соответствии с поисковым алгоритмом, если первая строка  может быть приведена к нулевой после r шагов из элементарных строчных операций, она будет назависимой от r верхних строк  , т.е. она не может быть представлена через r левых коэффициентов

С другой стороны, если первая строка  не может быть приведена к нулевой после rэлементарных строчных операций, она будет независимой от rверхних строк , т.е. она не может быть представлена через r левых коэффициентов

Так как поиск всегда приводит к наименьшему r, которое представляет наименьший порядок коэффициентов L(s) и M(s), порядки полученных матриц L(s) и M(s) будут наименьшими. Таким образом, мы доказали, что строчный поисковый алгоритм обеспечивает наименьший порядок решения (4) для первой строки. Так как это рассуждение может быть применено и к другим строкам , доказательство завершено. ▄

15.3. Синтез компенсатора

В этом разделе представлен синтез входного – выходного компенсатора, обеспечивающего заданный матричный знаменатель замкнутой системы F(s) минимального порядка. На примере будет проиллюстрирована процедура синтеза.

В разделе 15.2 было показано, что если  образует полное столбцовое пространство после удаления нулевых столбцов, для любой заданной  с i-ым столбцом степени меньше  матрица  со строчными степенями, равными . Таким образом, если  строчно приведенная, имеется уверенность, что C(s) правильная.

Условие того, что строчные степени больше или равны , достаточно, но не является необходимым. При заданном F(s) нижний порядок  с произвольно выбранным детерминантом может быть часто найден, в особенности в случае большого индекса наблюдаемости и/или большой размерности системы. Последующий синтез предполагает достижение наименьшего порядка компенсатора для заданного знаменателя замкнутой системы.

При синтезе вместо решения (4) применяют строчный поисковый алгоритм к расширенной результантной матрице  и ищут матрицу коэффициентов  такую, что

.

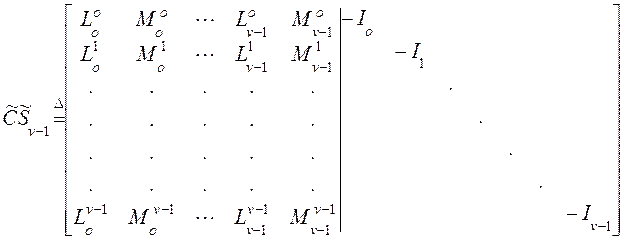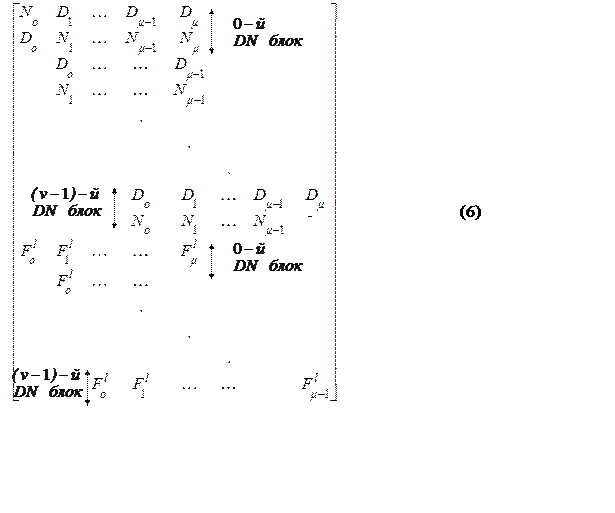Так как подматрица  имеет полный столбцовый ранг после удаления нулевых столбцов, все F блоки  должны быть зависимыми от DN блоков. Этот факт может быть замечен из тождественной матрицы в правой части .

Полученная матрица  должна быть проверена. Рассмотрим прежде всего первые строки F блоков в , которые соответствуют первым элементам  и . Если первые строки в j-ых Fблоках, , все зависят от 0-го до i-го DN блоков, тогда первая F строка будет в точности i-го порядка.