Другие предметы \ Многоканальные системы управления

Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 14

16.2. Постановка задачи

В данном разделе рассмотрим решение уравнения (1), где A(s)  (n*m), B(s) – (n*n) и C(s) – (n*n) – заданные полиномиальные матрицы с несингулярной матрицей B(s). Задача состоит в поиске пары полиномиальных матриц подходящей размерности, таких, чтобы удовлетворялось (1).

Мы далее будем предполагать, что A(s) и B(s) слева  взаимно простые, если это не имеет места, тогда для существования решения их наибольший общий левый делитель должен также быть левым делителем C(s).

Существование решения (1) следует из существования решения

где  единичная матрица. Если  – (1), тогда очевидно, что  также решение при выполнении условий

                            (2)

с  и , удовлетворяющими

                                                                                       (3)

где K(s) – любая произвольная матрица.

Далее если B(s) несингулярная и  правое взаимно простое разложение для , т.е.

                                                                           (4)

тогда для любого полиномиального решения (1) существует полиномиальное  K(s) такое, что (2) удовлетворяется.

Для случая, когда  столбцово приведенное, тогда  строго правильное (т.е. , если и только если

                                                  (5) Здесь  обозначает степень ой строки.

Наконец, отметим, что если  в (4) выбрана столбцово приведенной, тогда решение  с , удовлетворяющим (5), единственно. Это следует из того факта, что если как , так и  решения (1), тогда, как утверждалось выше, существует полиномиальная K(s) такая, что

                                                  (6)

Из того факта, что если  и  удовлетворяют (5), следует, что

строго правильное и поэтому K(s)=0.

16.3. Алгоритм

Пусть A(s), B(s) и C(s) заданы

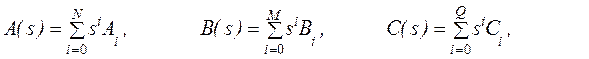                     (7)

где коэффициенты матрицы и

П р и м е ч а н и е. Пусть N=M=Q=2. Тогда возможный вид матриц A, B и С в формулах (7):

▄

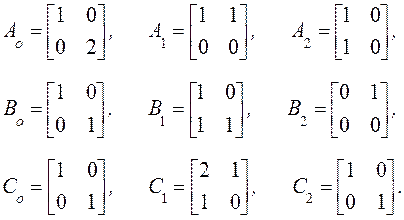
Мы можем предполагать без потери общности, что  несингулярная, поскольку если это не так, мы можем подставить в (1) новую переменную , где – любой скаляр, такой, что  Эта подстановка преобразует (1) в

где  и   несингулярное.

Ввиду несингулярности  возможно разложение в ряд Тейлора выражения  около s=0, т.е.

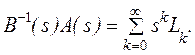                                                                                              (8)

П р и м е ч а н и е.  Частный случай для (8):

    ▄

Коэффициенты матрицы  удовлетворяют

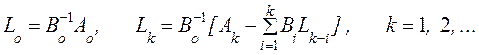                                 (9)

П р и м е ч а н и е. Продолжим вычисления из предыдущего примечания:

.

Приравняем коэффициенты при одинаковых степенях

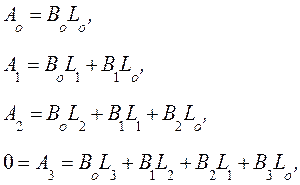
В последней формуле . Из полученных соотношений найдем :

▄

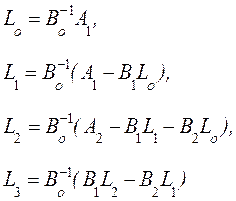
Аналогично,

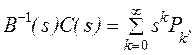                                                                               (10)

где  заданы

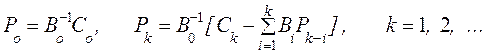                                      (11)

П р и м е ч а н и е. В развернутом виде формулы (11) выглядят так:

▄

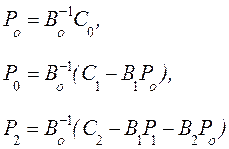
Решение  может быть записано в форме

                                             (12)

где – степень столбцово приведенной  в (4) и  еще подлежит определению. Если  столбцово неприведенная, тогда существует унимодальная  такая, что  столбцово приведенная.

Умножение (1) слева на  дает:

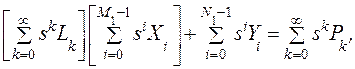                                                              (13)

Приравнивая коэффициенты при s в степенях от  до , где

                                                                                   (14)

мы получим совокупность из  линейных матричных уравнений, которые могут быть укомпонованы в следующее блочное матричное уравнение:

                                                            (15)

где  и – матрицы с элементами из IR размерами n(h-N1)*mM1,   n(h-N1)*n  и  mM1*n  соответственно,  определенные так:

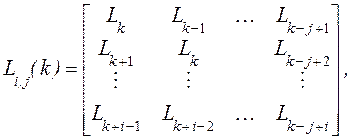                                            (16)

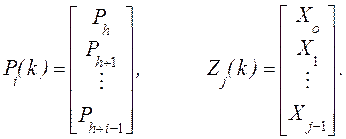
П р и м е ч а н и е. Пусть  Развернем формулу (13):

Здесь в ряде по L ограничились тремя членами, что будет обосновано ниже; это соответствует случаю, когда h=4, см. 14. В приведенном выражении приравняем коэффициенты при одинаковых степенях s:

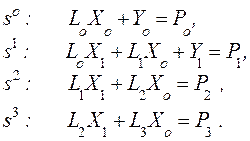
Эти уравнения можно записать в матричном виде (сравните с (15)):

Скачать файл