Сделаем
одно замечание по поводу степени компенсатора. При пространственном подходе
(через представление в пространстве состояний) размерность наблюдателя
состояния n-q. При использовании передаточных функций степень
компенсатора равна ![]() . Отметим, что строчный индекс
. Отметим, что строчный индекс ![]() матрицы G(s)
равен индексу наблюдаемости любого неприводимого представления G(s) и
имеет свойство
матрицы G(s)
равен индексу наблюдаемости любого неприводимого представления G(s) и
имеет свойство ![]() . Если p=q=1,
тогда
. Если p=q=1,
тогда ![]() и размерность наблюдателя состояния равна
степени компенсатора. Если
и размерность наблюдателя состояния равна
степени компенсатора. Если ![]() , тогда
, тогда ![]() ; если p<q, то
; если p<q, то
![]() может быть больше, равно или меньше
может быть больше, равно или меньше ![]() . Таким образом, результаты в области
пространства состояний и передаточных функций не идентичны.
. Таким образом, результаты в области
пространства состояний и передаточных функций не идентичны.
15. СИНТЕЗ КОМПЕНСАТОРА ТИПА «ВХОД-ВЫХОД ОБРАТНОЙ СВЯЗИ»
15.1. Введение
Для q*p строго правильного объекта G(s) с индексом наблюдаемости ![]() известно,
что достаточное условие достижимости произвольного размещения полюсов при
использовании единственной обратной связи является то, что порядок компенсатора
равен или больше чем
известно,
что достаточное условие достижимости произвольного размещения полюсов при
использовании единственной обратной связи является то, что порядок компенсатора
равен или больше чем ![]() Нижний порядок проектируемого
компенсатора продолжает оставаться в центре внимания научной литературы, однако
неизвестны публикации, успешно разрешившие этот вопрос. Предложен метод,
использующий результантную матрицу (resultant matrix) объекта, где нижний порядок компенсатора может быть
достигнут, если и только если матрица знаменателя замкнутой системы образует то
же пространство, что и результант наименьшего порядка. Однако неизвестно, как
выбирать матрицу знаменателя. В случае так называемой обратной связи типа
вход-выход (input-output feedback) матрица знаменателя замкнутой
системы разбивается на две части. Первая – знаменатель замкнутой системы,
вторая подлежит сокращению с числителем замкнутой системы. Эти идеи синтеза
лежат в основе метода, рассматриваемого в этом разделе. Знаменатель замкнутой
системы будет выбираться в первую очередь, затем компенсатор возможно меньшего
порядка может быть найден при помощи поисковых алгоритмов.
Нижний порядок проектируемого
компенсатора продолжает оставаться в центре внимания научной литературы, однако
неизвестны публикации, успешно разрешившие этот вопрос. Предложен метод,
использующий результантную матрицу (resultant matrix) объекта, где нижний порядок компенсатора может быть
достигнут, если и только если матрица знаменателя замкнутой системы образует то
же пространство, что и результант наименьшего порядка. Однако неизвестно, как
выбирать матрицу знаменателя. В случае так называемой обратной связи типа
вход-выход (input-output feedback) матрица знаменателя замкнутой
системы разбивается на две части. Первая – знаменатель замкнутой системы,
вторая подлежит сокращению с числителем замкнутой системы. Эти идеи синтеза
лежат в основе метода, рассматриваемого в этом разделе. Знаменатель замкнутой
системы будет выбираться в первую очередь, затем компенсатор возможно меньшего
порядка может быть найден при помощи поисковых алгоритмов.
15.2. Вспомогательные сведения
Рассмотрим задачу синтеза компенсатора типа «вход-выход обратной связи» (input-output feedback compensator). Для этого потребуются некоторые вспомогательные сведения.
Рассмотрим q*p строго правильный объект
![]()
где D(s) и N(s) – взаимно
простые справа и D(s) – столбцово приведенная со
столбцовыми степенями ![]() . Компенсатор «вход-выход
обратной связи» может быть записан так:
. Компенсатор «вход-выход
обратной связи» может быть записан так:
![]()
Структура системы представлена на рисунке.
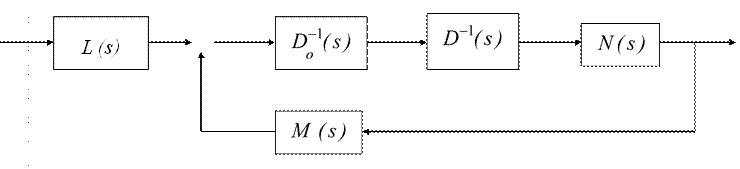 |
(–)
Следующая лемма указывает способ синтеза компенсатора.
Л е м м а 1. Рассмотрим проблему синтеза входного – выходного
компенсатора. Матрица знаменателя замкнутой системы может быть произвольно
назначена, если знаменатель компенсатора выбран строчно приведенным со
строчными степенями больше или равными ![]() , где
, где ![]() – индекс наблюдаемости объекта.
– индекс наблюдаемости объекта.
Ясно, что при таком методе синтеза порядок компенсатора будет
больше или равен ![]() Ниже приводится иллюстрация
процедуры синтеза. Первым делом выбираем желаемый знаменатель замкнутой системы
F(s). Без потери общности F(s) предполагается столбцово приведенной с теми же
столбцовыми степенями, что и D(s). К тому же, столбцовая степень коэффициентных матриц F(s) и D(s) одна и та же. Таким образом, столбцовые степени
Ниже приводится иллюстрация
процедуры синтеза. Первым делом выбираем желаемый знаменатель замкнутой системы
F(s). Без потери общности F(s) предполагается столбцово приведенной с теми же
столбцовыми степенями, что и D(s). К тому же, столбцовая степень коэффициентных матриц F(s) и D(s) одна и та же. Таким образом, столбцовые степени
![]()
должны быть меньше, чем соответствующие столбцовые степени F(s) и D(s). Далее выбираем гурвицеву матрицу Dс(s) в соответствии с леммой 1. После этого решаем уравнение
![]() (1)
(1)
с целью поиска матриц L(s) и M(s). Передаточная функция всей системы
![]() .
(2)
.
(2)
Подстановка (1) в (2) дает
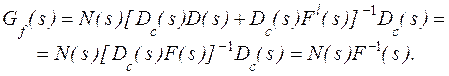 (3)
(3)
Так как ![]() гурвицева, сокращение
гурвицева, сокращение ![]() допустимо. Таким образом, синтез окончен.
допустимо. Таким образом, синтез окончен.
При поиске компенсатора главная процедура состоит в решении (1). Для реализации этой процедуры предлагается использовать строчный поисковый алгоритм. Алгоритм должен быть применен к расширенной результантной матрице
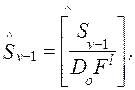
где
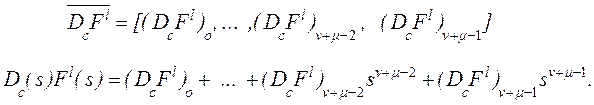
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.