В последней матрице старшие строчные
степени расположены па диагонали, что было достигнуто умножением на ![]()
![]() , но в данном случае
, но в данном случае ![]() , вопреки требованию
, вопреки требованию ![]() для всех
для всех ![]() . Чтобы
исправить положение, мы сейчас используем так называемые несущественные
состояния (non-essential states). Для этого сперва сделаем недиагональные
элементы второй строки нулевыми при помощи элементарных операций, что
соответствует умножению уравнения
. Чтобы
исправить положение, мы сейчас используем так называемые несущественные
состояния (non-essential states). Для этого сперва сделаем недиагональные
элементы второй строки нулевыми при помощи элементарных операций, что
соответствует умножению уравнения
![]()
слева на матрицу ![]() :
:
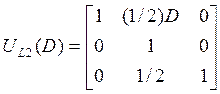 .
.
Получили:
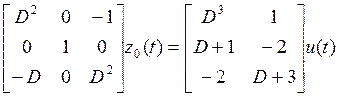 .
.
![]()
![]()
![]()
![]()
Как следует из полученной системы,
вторая компонента ![]() вектора
вектора ![]() соответствует
алгебраическому, а не дифференциальному уравнению
соответствует
алгебраическому, а не дифференциальному уравнению ![]() (она
не зависит от производных
(она
не зависит от производных ![]() ), следовательно, она не
является существенным состоянием. Вы разим
), следовательно, она не
является существенным состоянием. Вы разим ![]() через
через ![]() :
:
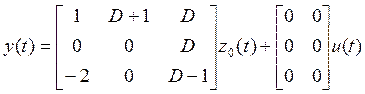 .
.
![]()
![]()
Подставим ![]() в
в ![]() :
:
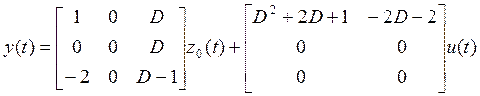 .
.
![]()
![]()
Шаг 3. По известным ![]() и
и
![]() находим
находим ![]() :
:
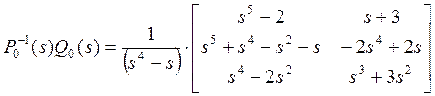 .
.
Выделим полиномиальную часть ![]() из полученной передаточной функции,
используя формулу деления
из полученной передаточной функции,
используя формулу деления ![]() , где
, где ![]() - делимое,
- делимое, ![]() -
делитель,
-
делитель, ![]() - частное и
- частное и ![]() -
остаток:
-
остаток:
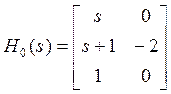 ,
, 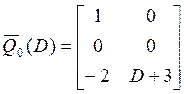 .
.
Шаг 4. Зная ![]() и
и ![]() , входящие в уравнение
, входящие в уравнение
![]() , можем найти эквивалентное описание в
пространстве состояний:
, можем найти эквивалентное описание в
пространстве состояний:
![]() ,
, ![]() .
.
В матрице ![]() , равной
, равной
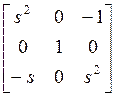 , исключаем вторую переменную и
представляем ее в специальном виде:
, исключаем вторую переменную и
представляем ее в специальном виде:
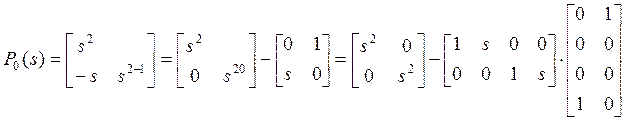 .
.
![]()
![]()
![]()
В матрице 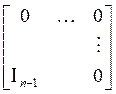 , где
, где ![]() , второй и четвертый столбцы меняем на
столбцы матрицы
, второй и четвертый столбцы меняем на
столбцы матрицы ![]() :
:
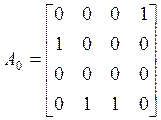 .
.
В матрице ![]() выбрасываем
вторую строку, получаем матрицу
выбрасываем
вторую строку, получаем матрицу ![]() размерами 2*2, которую
представляем в виде
размерами 2*2, которую
представляем в виде ![]() :
:
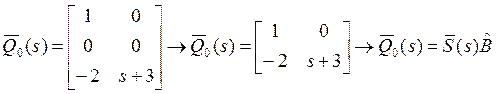
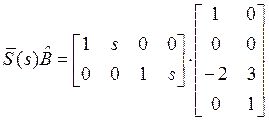 .
.
![]()
![]()
В нашем случае ![]() ,т.е.
,т.е. ![]() найдено.
Осталось найти
найдено.
Осталось найти ![]() : для этого в матрице
: для этого в матрице ![]() второй четвертый столбцы следует заменить
на столбцы матрицы
второй четвертый столбцы следует заменить
на столбцы матрицы ![]() . Далее остается вспомнить, что
вторая переменная была выброшена:
. Далее остается вспомнить, что
вторая переменная была выброшена:
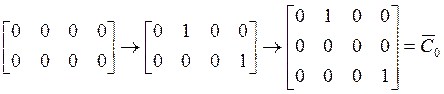
6. Реализация полиномиальных представлений
Теорема. Любая ![]() рациональная
матрица
рациональная
матрица ![]() может быть представлена как
может быть представлена как ![]() (или
(или ![]() ), где
любой наибольший общий правый делитель для
), где
любой наибольший общий правый делитель для ![]() и
и ![]() - унимодальная матрица (любой наибольший
общий левый делитель соответственно для
- унимодальная матрица (любой наибольший
общий левый делитель соответственно для ![]() и
и ![]() ).
).
Доказательство. Ввиду дуальности нужно доказать
только то, что ![]() может быть представлено как
может быть представлено как ![]() , где
, где ![]() и
и ![]() - относительно простые справа. Итак, нужно
показать, что возможно представление
- относительно простые справа. Итак, нужно
показать, что возможно представление
![]() , где
, где ![]() . Здесь
. Здесь
![]() и
и ![]() -
относительно простые полиномы. Найдем наименьший общий знаменатель
-
относительно простые полиномы. Найдем наименьший общий знаменатель ![]() ,
, ![]() столбца
столбца
![]() и составим матрицу
и составим матрицу ![]() .
Далее найдем представление
.
Далее найдем представление ![]() , где
, где ![]() (
(![]() делится
делится
![]() !). Если
!). Если ![]() -
некоторая неунимодальная матрица, являющаяся наибольшим общим правым делителем
для
-
некоторая неунимодальная матрица, являющаяся наибольшим общим правым делителем
для ![]() и
и ![]() , тогда
, тогда
![]() , где
, где ![]() ,
, ![]() . Таким образом, найдена минимальная
реализация
. Таким образом, найдена минимальная
реализация ![]() ■
■
Пример. Найдем представление в форме минимального дифференциального оператора и минимальное представление в пространстве состояний для матричной передаточной функции
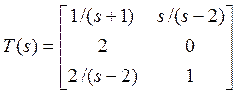 .
.
Произведем ряд вычислений:
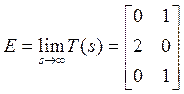 ,
,
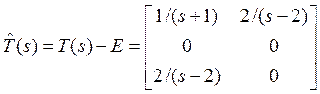 .
.
Здесь ![]() -
строго правильная часть
-
строго правильная часть ![]() . Найдем наименьшее
общее кратное знаменателей первого и второго столбцов:
. Найдем наименьшее
общее кратное знаменателей первого и второго столбцов: ![]() ,
,
![]() . Переходим к вычислению матриц
. Переходим к вычислению матриц ![]() и
и ![]() :
:
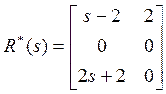 ,
, 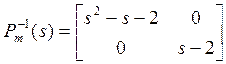 ,
, ![]() .
.
Оказалось, что ![]() и
и ![]() взаимно
простые справа, т.е.
взаимно
простые справа, т.е.
![]() ,
, ![]() .
.
Первая часть задачи решена. Для решения второй части задачи приравняем:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Далее применяя ранее изложенную процедуру, находим:
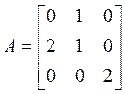 ,
, 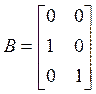 ,
, 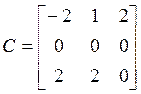 ,
, 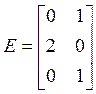
7. Характеристический полином и характеристические матрицы
Здесь представлена эффективная вычислительная процедура определения коэффициентов передаточной функции, базирующаяся на матрице наблюдаемости и близкая к методу Крылова (method Krilov). Метод может быть использован для определения характеристического полинома одноканальной системы.
Для представленной системы в пространстве состояний
![]() (1)
(1)
![]() ,
(2)
,
(2)
где ![]() - вектор
состояний,
- вектор
состояний, ![]() - матрица состояний (state transfer
matrix),
- матрица состояний (state transfer
matrix), ![]() - матрица управления (control transfer
matrix),
- матрица управления (control transfer
matrix), ![]() - входная переменная,
- входная переменная, ![]() - выходная переменная,
- выходная переменная, ![]() - вектор коэффициентов выхода,
- вектор коэффициентов выхода, ![]() - передаточный коэффициент «вход-выход»,
разработать процедуру генерации коэффициентов передаточной функции от
- передаточный коэффициент «вход-выход»,
разработать процедуру генерации коэффициентов передаточной функции от ![]() к
к ![]() .
.
Можно записать ![]() выражение для
выражение для ![]() и ее
производных через вектор состояний, вход и его производные:
и ее
производных через вектор состояний, вход и его производные:
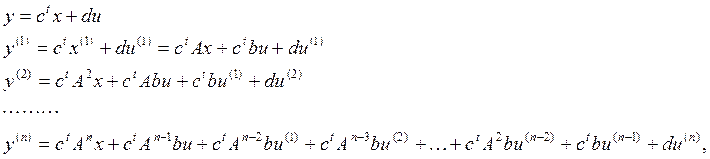
что эквивалентно
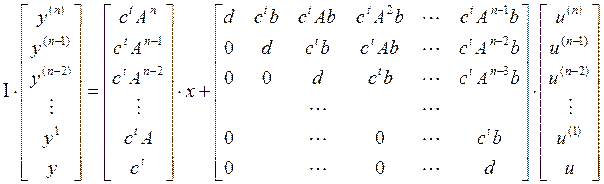
или
![]() ,
(3)
,
(3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.