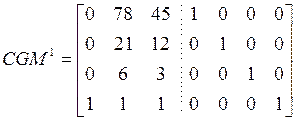Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 6

, и результирующая верхнетреугольная форма

.

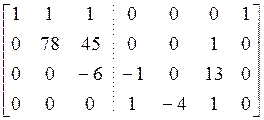Мы видим, что ранг  равен трем и что проверка правильности нашего выбора  подтвердилась. Мы можем отсюда сделать вывод о том, что нижняя строка действительно дает коэффициенты характеристического полинома , и

.

8.  Преобразование матрицы к строчно-приведенному виду

12.2. Преобразование матрицы к строчно  приведенному виду

Каждая несингулярная квадратная полиномиальная матрица  может быть преобразована к строчно приведенному виду исключительно столбцовыми операциями. Другими словами, существуют унимодальные матрицы  и  такие, что  и  строчно приведенные. Процедура преобразования  к эрмитовой форме (Hermite form) посредством элементарных столбцовых операций может быть использована для вычисления матрицы . В этом разделе мы обсудим одну из известных процедур вычисления .

Пусть  – полиномиальная матрица размерами (p * p) со строчными степенями , обозначаемыми как  Обозначим

.

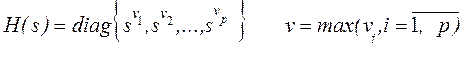Мы запишем

                                    (12)

                                               (13)

где   – единичная матрица. Мы отметим, что большинство строк  нулевые. Матрица  строчно приведенная, если и только если  несингулярная. Мы сформируем строчную матрицу

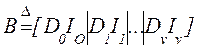                                                            (14)

и поставим в соответствие каждой строке В ее строчную степень .

Алгоритм:

Шаг 1.  Переставим строки  В и соответствующие им  так, чтобы  .

Шаг 2. Найдем ненулевой элемент, называемый ведущим элементом (pivot element), в первой строке  и затем исключаем, используя элементарные строчные операции над В, все элементы ниже его. Затем находим ненулевой ведущий элемент во второй строке  и исключаем все элементы ниже его. Повторяем эту процедуру до достижения последней строки . Если  появится нулевая строка, идти на шаг 3. Если нулевая строка не появилась в, идти на шаг 4.

Шаг 3. Если нулевая строка  появилась в, аналогичная строка в , будет также нулевой. Мы смещаем эту строку из В налево на 2pпозиций и уменьшаем соответствующее  на 1 и идем на шаг 1.

Шаг 4. По полученным ,  и  формируем

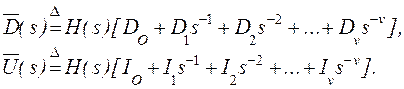
После этого имеем , причем  строчно приведенная.

П р и м е р.  Рассмотрим

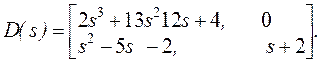
Мы запишем

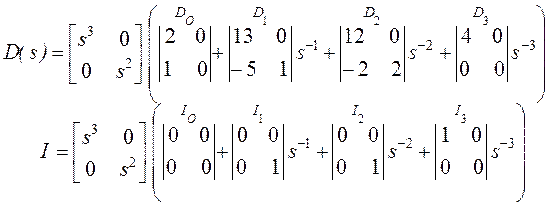
и сформируем

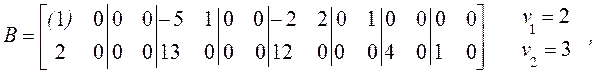
Мы выбрали ведущий элемент первой строки в  (отмечен скобками). Затем приведем элемент, расположенный ниже, к нулю, вычтя из второй строки В произведение первой строки В на 2:

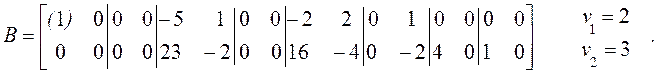
После этого смещаем вторую строку В на четыре позиции влево и уменьшаем  на 1:

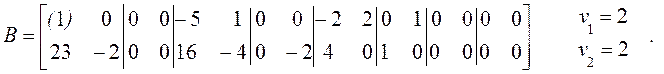
Ясно, что новое  невырожденное; следовательно, мы получили

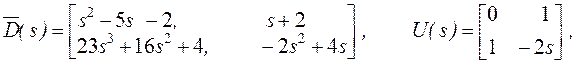
где - строчно приведенная.

П р и м е ч а н и е. Очевидно, что алгоритм, приведенный в этом разделе, может быть модифицирован таким образом, чтобы находить унимодальную матрицу V(s) такую, что D(s)V(s) , будет столбцово приведенной. Заданное разложение D^-1(s)N(s), если N(s) дано в соответствии с (12) и В(s) в соответствии с (14), может быть представлено так:

Таким образом, алгоритм приводится к

где  строчно приведенная матрица.

9.  Вычисление матричной передаточной функции многоканальной системы

14.1. Введение

При проектировании многоканальных линейных систем с постоянными параметрами желательно иметь описание системы в виде матричной передаточной функции системы.

При заданных динамических уравнениях в пространстве состояний порядка n в предположении их невырожденности, матричная передаточная функция может быть вычислена в два этапа. Прежде всего находят коэффициенты характеристического полинома, используя метод матрицы управляемости. Во-вторых, находят коэффициенты матричной передаточной функции, используя преобразование описания матрицы системы к сопровождающей форме.

Уравнение динамики для системы n-го  порядка с постоянными во времени параметрами могут быть записаны в следующем виде:

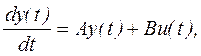                                                             (1а)

                                                                        (1б)

где y(t) –  n-мерный вектор состояния системы, u(t) – m-мерный вектор выхода системы.