Любая из интерактивных программ, таких, как MACSYMA и MATHLAB, может обеспечить требуемые вычисления для получения матричной передаточной функции.
Алгоритм может быть удобно записан в обозначениях MATHLAB, что и сделано ниже. Программа вычисляет матричную передаточную функцию системы n-го порядка с m входами и k выходами. Вход для программы должен быть представлен в виде системы {A, B, C}. На выходе будут появляться коэффициенты полинома в порядке возрастания степеней s в векторе Q и полиномы числителя в матрице H соответственно. Численный пример, приведенный следующем подразделе, был получен с использованием этой программы.
П р о г р а м м а
//---------------------------------------------------------------------------------------------// вычислить МПФ, Q & H, из A, B, C
//---------------------------------------------------------------------------------------------//
// N – состояний, M входов, К выходов
//
[N, M]=SIZE(B); [K, N]=SIZE(C);
// вычислить матрицу управляемости W
//
W=[B(:,1), ONES(N,N-1)];
FOR J=2: N DO W(:,J)=A*W(:,J-1);
//
// вычислить характеристический полином Q, решая матричное уравнение
//
Q=-W\(A*W(:,N));
//
// вычислить матрицы преобразований М1, М2, …
//
TMP=ONES(N);
FOR I=1: M DO ..
TMP(:,N)=B(:,I); ..
FOR J=(N-1): -1: 1 DO ..
TMP(:,J)=A*TMP(:,J+1)+Q(J+1)*(:,I); ..
END; ..
>[‘M’,I,’=TMP;’1<; //макро для формирования M1, M2, ..
TMP=[ ];
//
// вычисление числителя матричной передаточной функции H
//
H=ONES(K, N*M);
FOR I 1:M DO H(:, 1+(I-1)*N; I*N) =>[‘C*M’,I,’;’]<;
//-----------------------------------------------------------------------------------------------П р и м е р. Для иллюстрации предыдущих рассуждений пусть пространственное описание системы будет
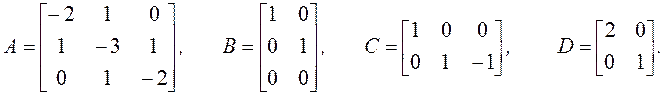
Так как матрица управляемости W1 для пары (А, b1) не вырождена, то

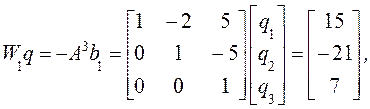
откуда ![]() . Таким образом,
. Таким образом,
![]()
Найдем ![]() :
:
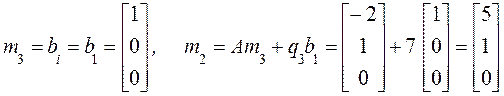 .
.
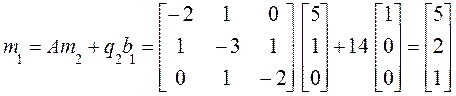 .
.
Получили
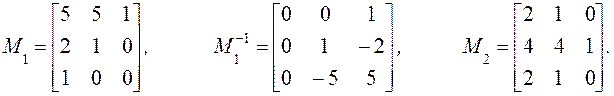
Тогда матричная передаточная функция системы
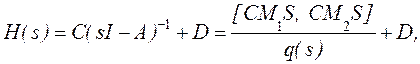
где для примера покажем
вычисление ![]() :
:
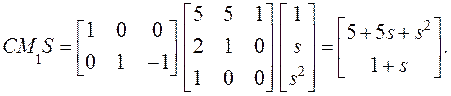
Имеем
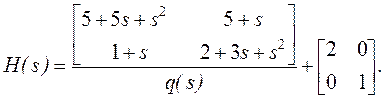
К тому же, так как М1 не сингулярная, она может быть использована для преобразования координат к стандартной форме. Соответствующие матрицы в координатной форме

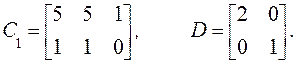
14.4. Выводы
В этом разделе представлена концептуально простая методика определения матричной передаточной функции многоканальной системы. Она вычисляется с использованием метода матрицы управляемости и преобразования к стандартной форме, даже если матрица преобразования сингулярная. Если матрица преобразования не сингулярная, она может быть использована как основа для преобразования координат к стандартной форме. Представлена программа вычисления матричной передаточной функции на «языке» MATHLAB.
10. Синтез компенсатора типа «вход-выход обратной связи»
В данном курсе лекций устройства, вводимые в систему автоматического управления часто называемые устройствами управления, корректирующими устройствами, будем называть компенсаторами, термин, который не так часто используется, но позволяет подчеркнуть функции, выполняемые им. Структура компенсаторов, методы их введения могут быть самыми разнообразными.
Компенсатор типа «вход- выход»
Одноканальный случай. Здесь рассмотрим случай компенсатора другого типа (рс.5.1)
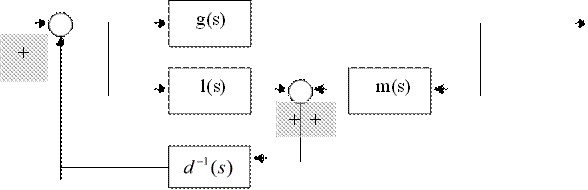 |
Рис.5.1. Система с компенсатором типа «вход- выход»
Передаточная функция от r к y
![]()
Определим ![]() или
или
![]()
Тогда ![]() .
.
Теорема
5.1. Рассмотрим объект с передаточной
функцией ![]() и
и ![]() . Для
любого
. Для
любого ![]() степени m и любого
степени m и любого ![]() степени m+n или меньше, существует правильный компенсатор
степени m+n или меньше, существует правильный компенсатор ![]() и
и ![]() такой, что система на рис.5.1 имеет передаточную
функцию
такой, что система на рис.5.1 имеет передаточную
функцию ![]() от r к y,
если и только если
от r к y,
если и только если ![]() и
и ![]() взаимно
простые и
взаимно
простые и ![]() .
.
При использовании теоремы (5.1) требуется решить (5.1) или
![]() (5.3)
(5.3)
Это диофантово уравнение и, следовательно, может быть приведено к системе линейных алгебраических уравнений.
Пусть
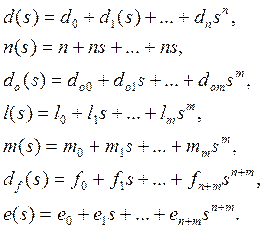 (5.4)
(5.4)
Уравнение (5.3) эквивалентно алгебраическому уравнению
![]() (5.5)
(5.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.