Из свойства структуры матрицы ![]() если F первые строк ограничены порядком i, зависимые коэффициенты в
если F первые строк ограничены порядком i, зависимые коэффициенты в ![]() -х F блоках,
-х F блоках, ![]() , могут быть выписаны
без вычислений.
, могут быть выписаны
без вычислений.
Такого же рода процедура может быть применена к другим F строкам. Следующая лемма указывает на требуемую степень компенсатора.
Л е м м а 3. Если i-ая строка заданной F(s) ограничена порядком ki, тогда существует правильный компенсатор
![]()
где ![]() произвольная диагональная матрица с i-ым диагональным элементом степени ki, удовлетворяющая (1).
произвольная диагональная матрица с i-ым диагональным элементом степени ki, удовлетворяющая (1).
Д о к а з а т е л ь с т в о. Если i-ая F
строка ограничена порядком ki, то
все i-ые F строки в r-х F блоках, ![]() , могут
быть линейно представлены через 0- ki – е DN блоки. Далее любая комбинация i-ых F
строк в r-х F блоках обладает тем же свойством. Таким образом, для любого
произвольного полинома
, могут
быть линейно представлены через 0- ki – е DN блоки. Далее любая комбинация i-ых F
строк в r-х F блоках обладает тем же свойством. Таким образом, для любого
произвольного полинома
![]()
существуют полиномиальные векторы Li(s) и Ni(s) со степенями, меньшими или равными ki, удовлетворяющие уравнению
![]()
где ![]() означает i-ую строку F(s). Таким образом доказано, что существуют полиномиальные
матрицы L(s) и N(s) со степенями i-ых L строки и N строки, меньшими или равными ki, удовлетворяющие (1), где
означает i-ую строку F(s). Таким образом доказано, что существуют полиномиальные
матрицы L(s) и N(s) со степенями i-ых L строки и N строки, меньшими или равными ki, удовлетворяющие (1), где ![]() выбраны в соответствии с леммой 3. Так как
выбраны в соответствии с леммой 3. Так как ![]() строчно приведенная, имеется уверенность в
правильности компенсатора.
строчно приведенная, имеется уверенность в
правильности компенсатора.
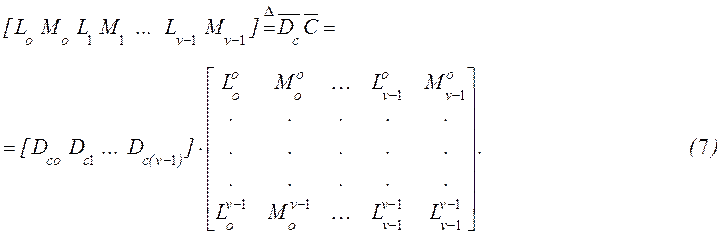
где ![]() - левая часть матрицы
- левая часть матрицы ![]() .
Отметим, что
.
Отметим, что
![]()
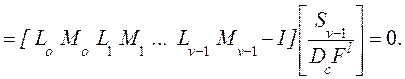
Это и есть как раз формула (4). Таким образом, (7) доказано. Синтез завершен. ▄
П р и м е р. Заданы объект управления
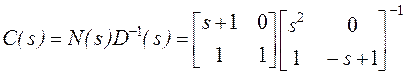
и желаемый знаменатель замкнутой системы
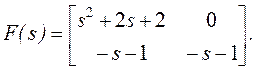
Мы
имеем 
Мы формируем
расширенный результант ![]() и решаем (6), используя строчный
поисковый алгоритм. Можно показать, что первая Fl строка ограничена 1-м порядком.
Далее выбираем
и решаем (6), используя строчный
поисковый алгоритм. Можно показать, что первая Fl строка ограничена 1-м порядком.
Далее выбираем 
С использованием (7) компенсатор может быть вычислен так
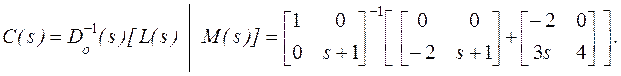
Получили правильный компенсатор первого порядка. ▄
З а м е ч а н и е 1. Метод синтеза из этого раздела
используют поисковый алгоритм над расширенной матрицей ![]() вместо
поискового алгоритма над расширенным результантом
вместо
поискового алгоритма над расширенным результантом ![]() в
типовом методе. Объем вычислений в стандартном методе и в рассматриваемом
методе практически одинаков.
в
типовом методе. Объем вычислений в стандартном методе и в рассматриваемом
методе практически одинаков.
З а м е ч а
н и е 2. Данный метод синтеза побуждает к более внимательному выбору
знаменателя замкнутой системы. По-видимому, знаменатель может быть выбран
последовательно от строки к строке. Можно попытаться использовать DN – блоки низкого порядка в ![]() с целью
уменьшения порядка компенсатора.
с целью
уменьшения порядка компенсатора.
З а м е ч а н и е 2. Рассматриваемый метод синтеза обеспечивает низкий порядок компенсатора, но необязательно минимальный порядок. Задача синтеза компенсатора минимального порядка довольно сложная и не до конца решена.
11. Решение матричного полиномиального уравнения
16.1. Введение
Рассмотрим решение матричного полиномиального уравнения
![]() (1)
(1)
Мы докажем теорему, касающуюся существования и
единственности решения ![]() для которого строки
для которого строки ![]() имеют минимально возможную степень.
имеют минимально возможную степень.
Возможно получение решения приведенного выше уравнения с
использованием элементарных левых и правых операций над полиномиальными
матрицами. Применением этих строчных операций ![]() может
быть приведено к диагональной форме (необязательно форме Смитта), в то время
как
может
быть приведено к диагональной форме (необязательно форме Смитта), в то время
как ![]() будет приведено к нижнетреугольному виду.
Сейчас решение (1) может быть получено решением множества скалярных
полиномиальных уравнений. К сожалению, этот способ довольно запутанный.
будет приведено к нижнетреугольному виду.
Сейчас решение (1) может быть получено решением множества скалярных
полиномиальных уравнений. К сожалению, этот способ довольно запутанный.
С намерением избежать сложности работы с полиномиальными матрицами мы прежде всего преобразуем матричное полиномиальное уравнение в систему линейных матричных уравнений. Следующий шаг состоит в уменьшении числа уравнений, подлежащих решению. Далее для разрешимости приведенной системы должно удовлетворяться некоторое ранговое условие. Наконец, получаем решение инвертированием некоторой квадратной матрицы минимально возможного порядка.
Важно напомнить роль, которую играет (1) в теории управления. Посредством представления матричной передаточной функции в виде произведения полиномиальной матрицы на обратную полиномиальной мы можем привести различные задачи синтеза такие, как стабилизация, модальный синтез и другие, к решению уравнения (1). Решение задачи оптимального управления и проблемы оптимальной фильтрации также сводится к решению указанного уравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.