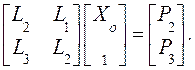
В обозначениях уравнения (16) это запишется так:
![]() ▄
▄
Т е о р е м
а 1. Необходимое и достаточное условие для того, чтобы ![]() было решением (1) с
было решением (1) с ![]() , удовлетворяющим условию (5) и
, удовлетворяющим условию (5) и ![]() есть
есть
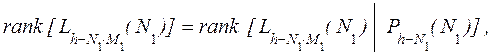 (17)
(17)
где ![]() и
и ![]() заданы уравнением (16).
заданы уравнением (16).
Д о к а з а
т е л ь с т в о. Если ![]() , заданное равенством (12), является решением (1),
тогда
, заданное равенством (12), является решением (1),
тогда ![]() должно удовлетворять (13). Условие (17) может быть рассматриваемо как
необходимое условие на ранг матрицы (15), при котором (15) имеет решение. Когда
условие (17) удовлетворяется, тогда решение (15) существует и
должно удовлетворять (13). Условие (17) может быть рассматриваемо как
необходимое условие на ранг матрицы (15), при котором (15) имеет решение. Когда
условие (17) удовлетворяется, тогда решение (15) существует и ![]() может быть получено. Матрица
может быть получено. Матрица ![]() может быть найдена приравниванием
коэффициентов первых
может быть найдена приравниванием
коэффициентов первых ![]() членов ряда s в (13), т.е.
членов ряда s в (13), т.е.
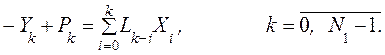 (18)
(18)
Мы еще
должны доказать, что ![]() образует решение (1). В намерении доказать это мы
прежде всего напишем блочное матричное уравнение, элементы которого –
вещественные числа:
образует решение (1). В намерении доказать это мы
прежде всего напишем блочное матричное уравнение, элементы которого –
вещественные числа:
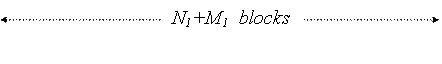
![]()
![]()
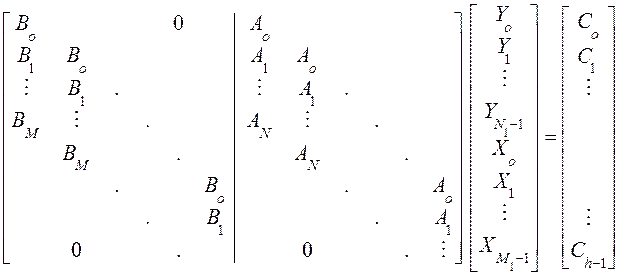 (19)
(19)
Умножим слева (19) на N1+1 блочную матрицу размерами (nh * nh), в намерении воспользоваться результатами из (10):
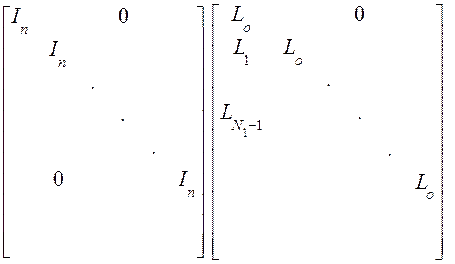
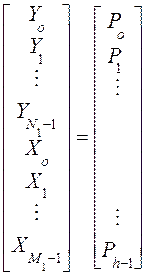 (20)
(20)
П р и м е ч а н и е. Развернем уравнение (1) для случая
![]()
Искомые
полиномиальные матрицы ![]() и
и ![]() имеют степени (12):
имеют степени (12):
![]()
Ранее они
были выбраны по единице , т.е. ![]() Запишем (1):
Запишем (1):
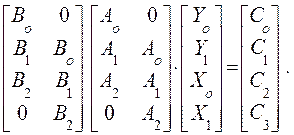 (191)
(191)
Это частный
случай (19). Поясним выкладки, связанные с получением (20). В (191)
первую строку (первое матричное уравнение) умножим слева на ![]() и учтем (9) и (11):
и учтем (9) и (11):
![]()
Первую
строку, умноженную слева на ![]() , сложить со второй:
, сложить со второй:
![]()
Вторую
строку умножить слева на ![]() и учесть (9), (11):
и учесть (9), (11):
![]()
С учетом того, что третье и четвертое уравнения не изменяли, система (191) запишется так (это частный случай (20)):
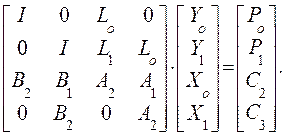 (201)
(201)
Продолжим
преобразования: умножим первую строку на ![]() , вторую на
, вторую на ![]() и прибавим к третьей. После умножения третьей строки слева на
и прибавим к третьей. После умножения третьей строки слева на ![]() и учета (19):
и учета (19):
![]()
умножим
вторую строку на ![]() и прибавим к четвертой
и прибавим к четвертой
![]()
умножим
третью на ![]() и прибавим к четвертой
и прибавим к четвертой
![]()
Наконец,
умножим четвертую на ![]()
![]()
Как следует из примечаний к формулам (9) и (10), последняя строка может быть записана более компактно:
![]()
В результате этих преобразований система (201) может быть записана следующим образом (сравните с (20)):
![]()
![]()
![]()
![]()
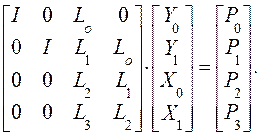 (202)
(202)
Это уравнение расщепляется на два:
![]()
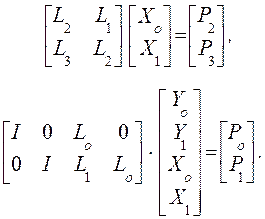
Из первого
уравнения (сравните с (15), (16)) находим ![]() , а из второго находим
, а из второго находим ![]() , для чего его следует переписать так:
, для чего его следует переписать так:
![]()
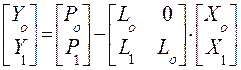
Блочное матричное уравнение составлено из (15) и (18). Таким образом, решение (15) и (18) есть также решение (20).
Из условия
(5) следует, что если степени некоторых строк ![]() меньше, чем
меньше, чем ![]() , тогда те же строки в
, тогда те же строки в ![]() (16) должны тоже иметь пониженную степень. Это
приводит к тому, что соответствующие столбцы
(16) должны тоже иметь пониженную степень. Это
приводит к тому, что соответствующие столбцы ![]() могут быть опущены, что, в свою
очередь, приводит к матрицам
могут быть опущены, что, в свою
очередь, приводит к матрицам ![]() и
и ![]() . Далее, переобозначая матрицу, составленную из
независимых строк
. Далее, переобозначая матрицу, составленную из
независимых строк ![]() через
через ![]() и матрицу, составленную из тех же
строк P через
и матрицу, составленную из тех же
строк P через ![]() , (15) можно переписать как
, (15) можно переписать как
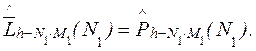 (21)
(21)
Из
единственности ![]() следует, что матрица
следует, что матрица ![]() должна быть квадратной и несингулярной.
должна быть квадратной и несингулярной.
В намерении
получить единственное решение ![]() мы увеличиваем на каждом шаге степень
мы увеличиваем на каждом шаге степень ![]() на единицу. Начиная с
на единицу. Начиная с ![]() , и затем проверяя существование решения (используя
ранговое условие) и продолжая эту процедуру до тех пор, пока условие (17) с
, и затем проверяя существование решения (используя
ранговое условие) и продолжая эту процедуру до тех пор, пока условие (17) с ![]() не удовлетворяется. Решение
не удовлетворяется. Решение ![]() далее получаем из решения (21) для
далее получаем из решения (21) для ![]() , т.е. для
, т.е. для ![]() и, наконец, для
и, наконец, для ![]() из (18).
из (18).
Следует заметить, что алгоритм может быть применен и для решения уравнения
![]()
посредством записи его в форме
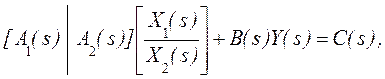
где ![]() необязательно квадратная матрица.
необязательно квадратная матрица.
П р и м е р.
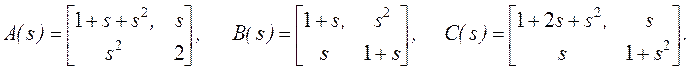
Из (9) и
(16) мы получим ![]() :
:
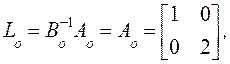
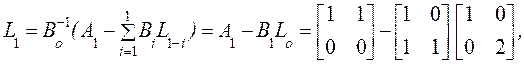
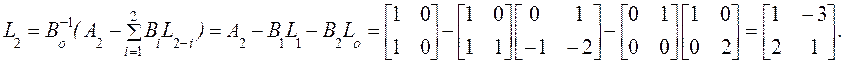 Выпишем матрицы
Выпишем матрицы ![]() :
:
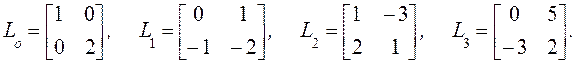
Перейдем к
уравнению (15) (здесь ![]() ):
):
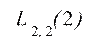 |
![]()
![]()

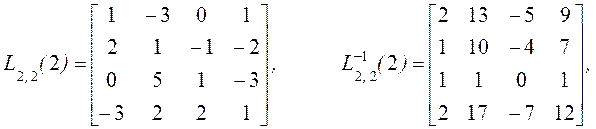
![]()
![]()
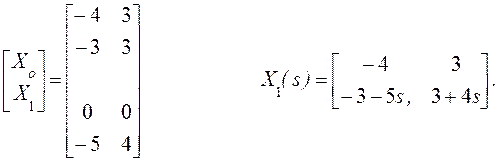
Из (11) мы получим
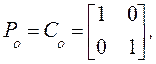
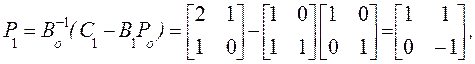
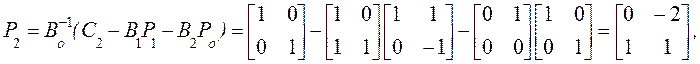

Найдем ![]() из (18)
из (18)
![]()
![]()
![]()
![]()

![]()
![]()
![]()

Единственное
решение, полученное из решения (16) для ![]() и (23) для
и (23) для ![]() , следующее:
, следующее:
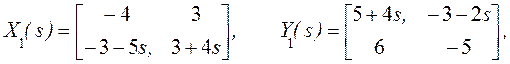
с рангом
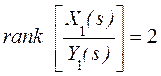
для всех s. Таким образом, ![]() и
и ![]() справа взаимно простые
справа взаимно простые
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.