![]() ,
,
![]() .
(3)
.
(3)
Как известно, такое преобразование не влияет на решение и на эквивалентность.
Шаг 2. Пусть ![]() , где
, где ![]() невырожденная матрица из коэффициентов при
высших степенях
невырожденная матрица из коэффициентов при
высших степенях ![]() строк матрицы
строк матрицы ![]() . Если
. Если ![]() , то
перейти к шагу 3. В противном случае подставим
, то
перейти к шагу 3. В противном случае подставим ![]() (это
не нарушает эквивалентность) в (3):
(это
не нарушает эквивалентность) в (3):
![]() ,
(4а)
,
(4а)
![]() .
(4б)
.
(4б)
Здесь ![]() ,
, ![]() ,
, ![]() .
Полиномиальная матрица
.
Полиномиальная матрица ![]() имеет ту особенность, что по ее
диагонали стоят элементы с высшими степенями по
имеет ту особенность, что по ее
диагонали стоят элементы с высшими степенями по ![]() в
каждой строке:
в
каждой строке:
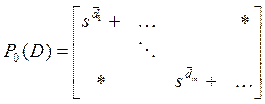 .
.
Здесь считаем, что ![]() для
для ![]() .
.
Шаг 3. Из (4а) находим
![]() .
.
Если ![]() -
строго правильная
-
строго правильная ![]() , то переходим к шагу 4. В
противном случае выделяем строго правильную часть
, то переходим к шагу 4. В
противном случае выделяем строго правильную часть ![]() из
из ![]() :
:
![]() , где
, где ![]() -
полиномиальная матрица. Здесь
-
полиномиальная матрица. Здесь ![]() - «остаток»:
- «остаток»:
![]()
![]() .
.
Определим ![]() и
подставим
и
подставим ![]() в (4а):
в (4а): ![]() . С
учетом введенного
. С
учетом введенного ![]() получаем
получаем ![]() .
Таким образом, система (4), если ввести
.
Таким образом, система (4), если ввести ![]() ,
запишется так:
,
запишется так:
![]() ,
(5а)
,
(5а)
![]() .
(5б)
.
(5б)
Шаг 4. Так как ![]() и
и ![]() определены, мы можем непосредственно
получить наблюдаемую реализацию
определены, мы можем непосредственно
получить наблюдаемую реализацию ![]() из строго правильной
передаточной матрицы
из строго правильной
передаточной матрицы ![]() системы (5). Перепишем
системы (5). Перепишем ![]() в виде
в виде
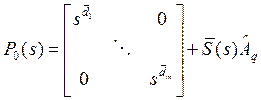 , где матрица
, где матрица ![]() размерами
размерами
![]() :
:
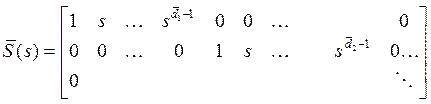 .
.
Здесь ![]() для
для ![]() и
и ![]() .
Вспомним соотношения:
.
Вспомним соотношения:
![]() ,
, ![]() ,
, ![]() .
.
Можно получить наблюдаемую реализацию
![]() для
для ![]() следующим
образом. Берем
следующим
образом. Берем ![]() ,
, ![]() ,
заменяем
,
заменяем ![]() - «штук» столбцов матрицы
- «штук» столбцов матрицы
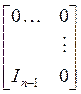 , а именно, столбцы с номерами
, а именно, столбцы с номерами ![]() на
на ![]() «штук»
столбцов матрицы
«штук»
столбцов матрицы ![]() и получаем матрицу
и получаем матрицу ![]() . С матрицей
. С матрицей ![]() проще -
проще -
![]() . Матрица
. Матрица ![]() вычисляется
так: заменим
вычисляется
так: заменим ![]() «штук» столбцов в нулевой матрице
«штук» столбцов в нулевой матрице ![]() , а именно столбцы с номерами
, а именно столбцы с номерами ![]() на
на ![]() «штук»
столбцов матрицы
«штук»
столбцов матрицы ![]() . Таким образом, получаем
наблюдаемую реализацию
. Таким образом, получаем
наблюдаемую реализацию ![]() для
для ![]() .
Другими словами, получили
.
Другими словами, получили
![]() ,
, ![]() .
(6)
.
(6)
Перейдем к переменной ![]() , а далее к
, а далее к ![]() :
:
![]() ,
, ![]() ,
, ![]() . (7)
. (7)
Таким образом, получили:
![]() , где
, где ![]() .
.
Шаг 5. Подставим (7) в (3б):
![]()
и используем зависимости (6) для исключения производных из правой части последнего уравнения, что дает
![]()
В результате
получено описание системы в уравнениях пространства состояний ![]() . Индекс «0» следует опускать, так как фактически система может быть и
ненаблюдаема
. Индекс «0» следует опускать, так как фактически система может быть и
ненаблюдаема
5. Примеры перехода от дифференциальных операторов к пространству состояний
Пример. Дано описание системы в виде (1) п.6:
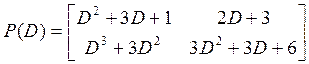 ,
, 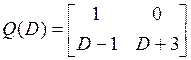 .
.
Матрица ![]() строчно
правильная, и поэтому нужно выполнить шаг 1. Матрицы
строчно
правильная, и поэтому нужно выполнить шаг 1. Матрицы ![]() ,
, ![]() и
и ![]() таковы:
таковы:
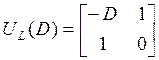 ,
, 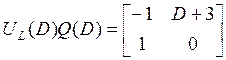 ,
, 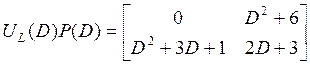 .
.
На шаге 2 вычисления начинаем
с матрицы ![]() и далее находим
и далее находим ![]() ,
,
![]()
![]() :
:
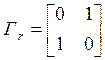 ,
, 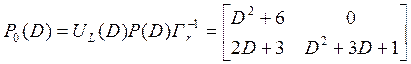 .
.
Шаг 3. Так как ![]() , то
, то ![]() - строго правильная и, следовательно,
- строго правильная и, следовательно, ![]() ,
, ![]() .
Вычисления на этом шаге пропускаем.
.
Вычисления на этом шаге пропускаем.
Шаг 4. Зная ![]() и
значения
и
значения ![]() , вычисляем матрицу
, вычисляем матрицу ![]() :
:
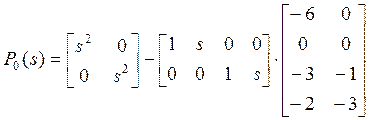 .
.
![]()
![]()
По известной ![]() находим
находим
![]() :
:
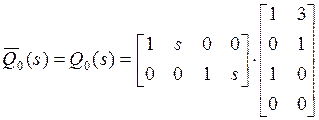 .
.
![]()
![]()
Проще с матрицей ![]() :
: ![]() . Для
вычисления
. Для
вычисления ![]() находим
находим ![]() ,
, ![]() . Учитывая то, что
. Учитывая то, что ![]() ,
найдем
,
найдем
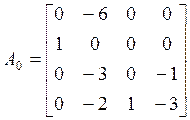 ,
,  ,
,
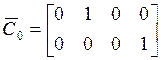 ,
, 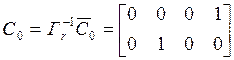 .
.
Матрица ![]() получена
заменой второго и четвертого столбцов матрицы
получена
заменой второго и четвертого столбцов матрицы ![]() на
первый и второй столбцы матрицы
на
первый и второй столбцы матрицы ![]() , а матрица
, а матрица ![]() получена заменой
получена заменой ![]() «штук»
столбцов матрицы
«штук»
столбцов матрицы ![]() . Получили описание
. Получили описание ![]() , эквивалентное дифференциальному
(полиномиальному) описанию.
, эквивалентное дифференциальному
(полиномиальному) описанию.
Шаг 5. Так как ![]() полностью
наблюдаема, можно последовательным дифференцированием
полностью
наблюдаема, можно последовательным дифференцированием ![]() ,
используя
,
используя ![]() , исключить все производные
, исключить все производные ![]() и получить
и получить ![]() .
Опишем эти действия более подробно.
.
Опишем эти действия более подробно.
Из ![]() следует:
следует:
![]() ,
, ![]() .
.
Так как
![]() , то, вычислив
, то, вычислив
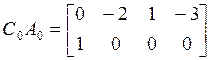 ,
, 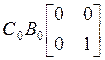 , получим
, получим
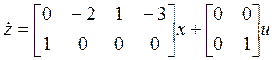 , откуда
, откуда
![]() ,
, ![]() .
.
Учтем, что ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Окончательно:
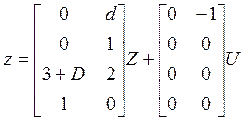 ■
■
![]()
![]()
Пример. Дано описание в виде (1):
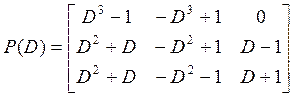 ,
,
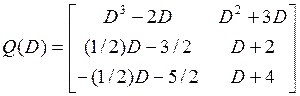 ,
,
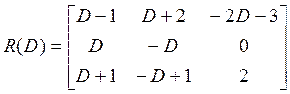 ,
, ![]() .
.
Шаг 1. Матрица ![]() строчно
неправильная: строчные степени
строчно
неправильная: строчные степени ![]() равны 3, 2, и 2, а
матрица
равны 3, 2, и 2, а
матрица ![]() вырожденная
вырожденная
 .
.
Приведем матрицу ![]() к строчно приведенному виду, для чего
подберем соответствующее унимодальное преобразование
к строчно приведенному виду, для чего
подберем соответствующее унимодальное преобразование ![]() и
вычислим ряд матриц:
и
вычислим ряд матриц:
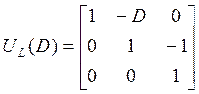 ,
, 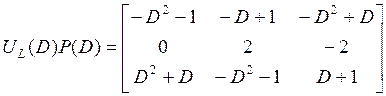 ,
,
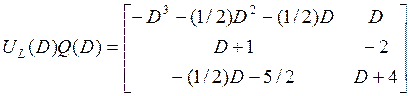 .
.
Шаг 2.Найдем ![]() и
и ![]() :
:
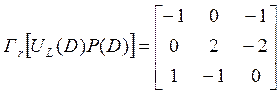 ,
, 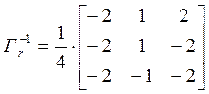 .
.
Вычислим ![]()
![]() :
:
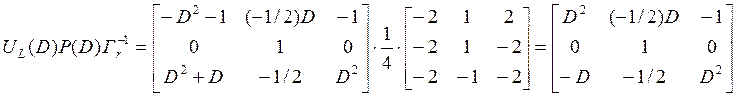 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.