Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 10

где  определено как в (2.11). Если , тогда  имеет полный столбцовый ранг. Отсюда для любого  решение  существует в (5.5). Решение немедленно дает правильный компенсатор.

Пример 5.1. Рассмотри объект с  передаточной функцией

Ясно, что мы имеем n=2 и  Допустим мы выбрали  и  Отметим, что степень  меньше, чем n+m=3. Вычислим

и сформируем систему

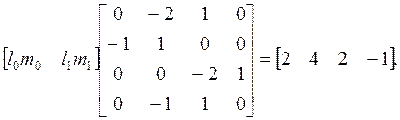
Ее решение  Отсюда компенсатор таков

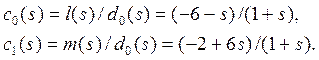
Получили правильные рациональные функции. Система показана на рис.5.2.

 

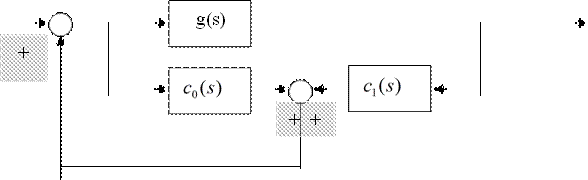Рис.5.2. Система с компенсатором типа «вход- выход» и не являющаяся хорошо устроенной

Недостатком системы является то, что хотя компенсатор и правильный, но в целом система включает в себя неправильные передаточные функции (найдите контур, передаточная функция которого соответствует неправильной передаточной функции). А это соответствует тому, что система не является хорошо устроенной.

Теорема 5.2. Рассмотрим объект с передаточной функцией    и  Для любой  степени m и любого  степени  n+m существует компенсатор  и  такой что система с обратной связью рис.5.2 хорошо устроена и имеет передаточную функцию  от r к y, если и только если  и  взаимно простые  .

Многоканальный случай. В этой части результаты, полученные для одноканального случая, будут перенесены на многоканальный случай. Рассмотрим систему, изображенную на рис. 5.2, но в предположении, что система многоканальная (рис.5.3). Пусть объект описывается p*q правильной рациональной матрицей . Компенсаторы соответствуют p*p правильной рациональной матрице

и p*q правильной рациональной матрице .

 

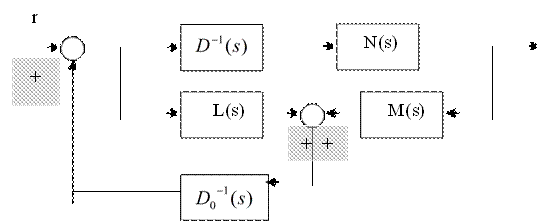Рис.5.3. Многоканальная система с компенсатором типа «вход- выход»

Передаточная матрица от r к y на рис.5.3 может быть вычислена

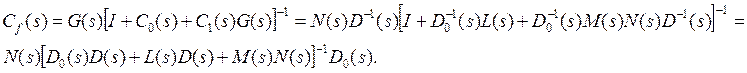(5.6)

Определим

                              (5.7)

                     (5.8)

Тогда  преобразуется к

                                             (5.9)

Зададим

                                            (5.10)

                                            (5.11)

Теорема 5.3. Рассмотрим q*p объект с правильной передаточной матрицей  Пусть - столбцовые степени , и пусть  строчный индекс . Пусть , при . Тогда для любой строчно приведенной матрицы  со строчными степенями  и любой  со свойством, что

                                         (5.12)

существует и невырождено, существует компенсатор с правильными рациональными матрицами  и . Система рис.5.3 с таким компенсатором хорошо устроена и имеет передаточную матрицу , если и только если  и  взаимно простые справа   столбцово приведенная.

При синтезе матрица-знаменатель компенсатора может быть выбрана как

                            (5.13)

где - произвольные гурвицевы полиномы степени .

Следствие 5.1. Рассмотрим q*p объект с правильной рациональной передаточной матрицей  Пусть  будут столбцовыми степенями , и пусть  строчный индекс . Тогда для любого со всеми строчными степенями, равными  и строчно приведенной, существуют компенсаторы с правильными рациональными матрицами  и  такими, что система рис.5.3 хорошо устроена и имеет передаточную матрицу , если и только если  и  взаимно простые справа   столбцово приведенная.

Применять теорему 5.3 и ее следствие следует непосредственно. Во- первых, мы используем матрицы коэффициентов матриц  и  для формирования матрицы :

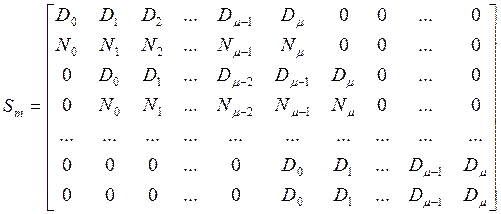                                          (5.14)

Далее находим линейно независимые строки  в порядке сверху вниз. Пусть  наименьшее целое число такое, что все N строк в последней блочной строке  линейно независимы. Это  есть строчный индекс . Для удобства мы положим  для всех i в теореме 5.3. Пусть

                                       (5.15)

                                 (5.16)

  (5.17)

где . Подстановка (5.15) – (5.17) в (5.8) дает

.                  (5.18)

Решение этой системы линейных алгебраических   уравнений и позволяет получить требуемый компенсатор.