Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 8

Если матрица общего вида (not derogatory), тогда пара (А, b) управляема для этого вектора b и матрица управляемости не вырождена.

А-инвариантное подпространство (А-invariant subspase) есть подпространство, ортогональное любому строчному вектору А.

Для того, чтобы показать необходимость условия 2, положим  равным строчному собственному вектору А, соответствующему собственному значению , тогда . Если b ортогонально, тогда   Это влечет  и, следовательно, строки W линейно зависимы, т.е. W сингулярно.

Как только q определено, стандартная формула матриц M, может быть вычислена переходом к многовходовой системе и алгоритму, основанному на рекурсивных формулах Леверье для каждой пары (A, b_i), где b_i – i-ый столбец  В,  Пусть М_i представлено в виде столбцов

, тогда

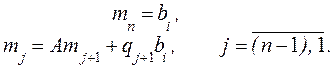                                                               (7)

Формулы (7) справедливы для любой матрицы А, как вещественной, так и комплексной, и стандартная форма матриц М_i, всегда существуют, хотя они могут быть вырожденными (сингулярными). Если матрица М_i не сингулярная, она может быть использована как базис для вычисления преобразования к стандартному виду. В общем случае стандартная форма не единственна и для практического использования может быть выбрана лучшая из нескольких возможных. В нашем случае стандартная форма зависит от входа, для которого система управляема.

14.3. Определение МПФ

Пусть матрицы (1) и (2) разбиты на столбцы следующим образом

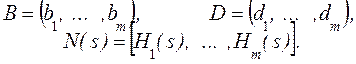                                              (8)

H_i(s) – столбцовый вектор длины k, соответствующий передаточной функции для каждого выхода при соответствующем входе U_i(s).

Из (2) тогда имеем

                                                                (9)

Пусть

                                            (10)

S – вектор-столбец размерности n, включающий соответствующие степени s;  q(s) – характеристический полином системы.

Полагая систему управляемой при конкретном входе u_i(t), можно найти q(s), используя метод матрицы управляемости (4). Для этого потребуется найти стандартную форму матрицы М_i, используя (7). Затем могут быть вычислены столбцы матричной передаточной функции следующим образом:

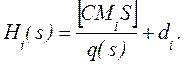                                                                                              (11)

Передаточные функции  составлены из линейных комбинаций строк М_i . Столбцы М_iсвязаны с коэффициентами соответствующих степеней s числителя . Таким образом, каждая строка М_iможет быть рассматриваема как вектор в n-мерном полиномиальном пространстве

Сравнение (5) и (7) указывает на то, что М_iподобна матрице управляемости W_iдля пары (A, b) . Так как столбцы М_i и W_i  (каждый набор) образуют одно и то же пространство,  М_i  будет сингулярным, только если b_i лежит в А-инвариантном подпространстве. Таким образом, ранг М_i  равен рангу W_i , который равен числу управляемых полюсов по входу u_i.

Матричная передаточная функция может включать неуправляемые и ненаблюдаемые моды, независимо от того, будет ли иметь место сокращение нулей и полюсов. Формула (11) может быть полезна для демонстрации эффекта обратной связи или вариации параметров системы на отдельные элементы H_ij . Кроме того, стандартная форма матрицы, приведенная здесь, играет фундаментальную роль в анализе эффекта обратной связи по состоянию через полюса и нули системы.

При формировании матрично-векторных произведений в (7), как показывает сравнение с матрично-матричными произведениями, используемыми в разложении Леверье, здесь уменьшено число требуемых умножений (и сложений) с 0(n⁴) до 0(n³). Количество требуемых  операций для получения коэффициентов q, по методу матрицы управляемости из п. 14.2, включая решение линейной системы (4) методом исключения Гаусса, также равно 0(n³). Это тот же порядок, что и в большинстве существующих эффективных методов вычисления канонических форм, использующих элементарные матричные операции и для вычисления характеристического полинома и матричной передаточной функции. Для вычисления элементов матричной передаточной функции для системы n-го порядка с m входами и k выходами общее число требуемых операций умножения по методу, изложенному здесь, равно 0(n³)+mn²(k+n), в то время как по процедуре Леверье это число равно 0(n⁴)+mn²(k+n).