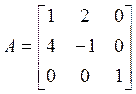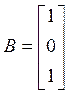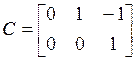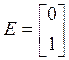Управляемая и наблюдаемая сопровождающие формы. Структурная теорема. Реализация матричной передаточной функции. Представление дифференциальными операторами. Примеры перехода от дифференциальных операторов к пространству состояний. Решение матричного полиномиального уравнения, страница 2

,   ,   ,   , найти передаточную функцию и правое полиномиальное разложение. Прежде всего, проверяем систему на управляемость и находим матрицу Q и управляемую каноническую форму:

,   ,   ,

,   .

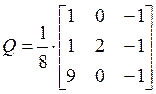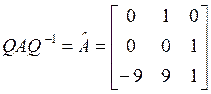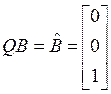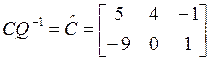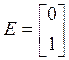Так как m = 1 (скалярный случай),  d₁ = 3 =  σ₁ = n, то

,   ,   ,

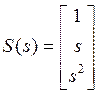, откуда несложно найти передаточную функцию

.

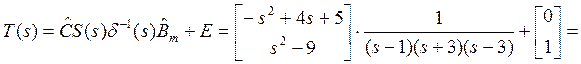
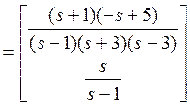Остается найти правое полиномиальное разложение:

,

,

  ■

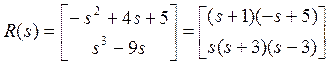Примечание. Можно использовать сопровождающую наблюдаемую форму для перехода от  к  :

, где матрица - невырожденная и такая, что  имеет вид сопровождающей наблюдаемой формы. Можно получить теорему, аналогичную приведенной выше, где  имеет вид  и вместо  использована  такая, что  имеет вид .

3.  Реализация матричной передаточной функции

Определение. Реализацией матричной передаточной функции T(s) любое представление в пространстве состояний {A, B, C, E}, чья матричная передаточная функция есть T(s).

В частности, реализации могут быть управляемые, наблюдаемые, минимальные, в каноническом и не в каноническом виде.

Для правильной передаточной функции T(s) = [t_{i j}(s)], где

, найдем наименьший общий знаменатель (least common denominator) j-го столбца g_j(s). Тогда справедливо

, где  получаем умножением  на . Можно использовать структурную теорему для получения описания в пространстве состояний:

.

В нашем случае  столбцово правильная

, т.е. можем положить

, ,

Но так как , то . Введем обозначения :

.

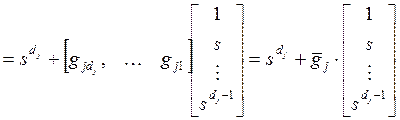Тогда

 (1)

               

По матрице  имеется возможность восстановить матрицу А в управляющей сопровождающей форме, т.е. восстановить А₀ . Развернем

и учтем, что из правильности T(s) следует

.

Таким образом, можем найти матрицу Е:

                                       .                                         (2)

Из (1), (2) и

следует

.

Последнее соотношение позволяет найти .

Пример. Найдем управляемую реализацию передаточной функции:

.

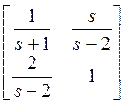Наименьший общий знаменатель первого и второго столбцов, а также матрица  равны

g₁(s)=(s+1)(s-2),  g₂(s)=s-2,  (d₁=2, d₂=1)

.

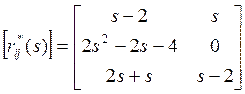Вспомним формулу  и развернем

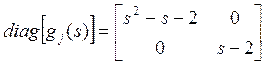, что после подстановки в (1) дает

   

.

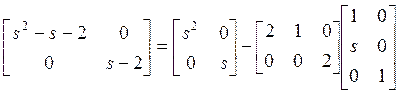Вычислим матрицу Е:

.

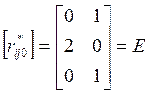Найдем :

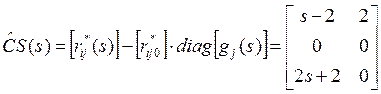, откуда несложно получить :

.

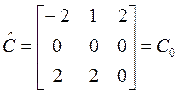По известным  и  найдем  , а из  определим :

,  .

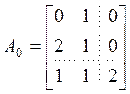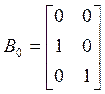Матрицы  найдены. ■

Справедливы следующие теоремы.

Теорема. n-мерная реализация {A, B, C, E} матрицы T(s)минимальная тогда и только тогда, когда она управляема и наблюдаема, т.е. когда размерности пространств управляемости θ и наблюдаемости  равны n: p[θ]=p[D].

Теорема. Если {A, B, C, E} – минимальная реализация для T(s), тогда  минимальная реализация в том и только том случае, если эти две реализации эквивалентны, т.е. существует такое невырожденное преобразование Q, при котором.

4.  Представление дифференциальными операторами

Часто используется описание в виде

                                                 ,                                                  (1а)

                                              ,                                            (1б)

где  - оператор дифференцирования;  - невырожденная матрица размером ;  -  матрица размером  и ,  - матрицы размерами  и . Возникает естественный вопрос о переходе к представлению в нормальной форме

                                           ,  ,                                           (2)

и наоборот. Как нетрудно увидеть, матричная передаточная функция системы, вычисленная по (1) и (2):

,

.

Вектор  можно восстановить по  и  при помощи некоторых матриц и

в случае полной наблюдаемости системы.

Естественным является вопрос о переходе от одного описания к другому, но так, чтобы при одном и том же входном сигнале на входе можно было выбрать такие начальные условия в этих системах, при которых выходы этих систем совпадали. Такие системы будем называть эквивалентными. Справедлива

Теорема. Любой дифференциальный оператор системы в форме (1) имеет эквивалентное представление в пространстве состояний (2).

Процедура перехода от (1) к (2) состоит в следующем:

Шаг 1. Если строчно правильная переходим к шагу 2. Если строчно неправильная, умножим (1а) слева на унимодальную матрицу такую, что  строчно правильная