Матричная передаточная функция, ассоциированная с (1), может быть получена с помощью преобразования Лапласа, и достаточно известный результат следующий:
![]() (2)
(2)
В общем случае H(s) – это (k*m) – матричная передаточная функция. Каждая передаточная функция – это соотношение полиномов комплексной переменной s. Типичный элемент H(s) имеет форму
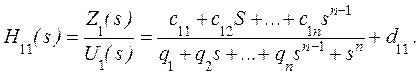 (3)
(3)
Известные в настоящее время методы вычисления матричной передаточной функции в большинстве своем базируются на рекурсивных формулах Леверье – Саура – Фаддеева – Фрама ( Leverrier – Souriau – Faddeeva – Frama) для резольвентной матрицы (sI-A)-1. Эти формулы были адаптированы для ряда программ для цифровых машин. К тому же алгоритм Леверье может быть использован даже в случае, если матрица А вырожденная и коэффициенты характеристического полинома, так же как и присоединенная матрица, вычисляются одновременно. По этим причинам указанный алгоритм используется при анализе цепей и в теории управления. Но одним из неудобств является то, что число требуемых умножений (и сложений) равно 0(n4).
Здесь используется алгоритм Леверье для получения алгоритма вычисления матричной передаточной функции. Рассматриваемый метод требует лишь только 0(n3) умножений (и сложений). Это значение того же порядка, какое требуется в наиболее эффективных существующих алгоритмах для вычисления канонических форм, использующих элементарные матричные операции для вычисления характеристического полинома. При использовании этого метода передаточная функция H(s) для (2) может быть получена в два этапа, а именно методом матрицы управляемости и стандартной формы. Стандартная форма, как будет показано выше, играет специальную роль в определении матричной передаточной функции, даже если матрица М сингулярная. Смысл этого метода может быть выявлен в терминах векторных пространств, ассоциированных со строками и столбцами М.
14.2. Преобразование к канонической форме
Каноническая форма – это очень удобное описание как для оценки характеристического полинома системы, так и для определения матричной передаточной функции. Исследования по приведению к различным каноническим формам и по вычислению характеристического полинома как для одноканальных систем, так и для многоканальных систем остается в центре исследований. Метод, представленный здесь, предполагает, что в первую очередь требуется найти коэффициенты характеристического полинома. Эффективный метод для вычисления характеристического полинома для одновходовой управляемой системы был введен в семидесятые годы и включает решение следующего уравнения для q с использованием метода исключения Гаусса (Gauss).
![]() (4)
(4)
где b– вектор-столбец размерности n, W – матрица управляемости для пары (A, b)
![]() (5)
(5)
и q представляет вектор коэффициентов характеристического полинома матричной передаточной функции
![]() (6)
(6)
Метод (4) может быть обобщен на многовходовые системы общего (стандартного) вида посредством выбора в качестве b одного из столбцов матрицы B (1), соответствующего такому входу, для которого система управляема. Однако возможен выбор b такого, при котором матрица управляемости имеет минимальное значение числа обусловленности. Таким образом, выбор b должен быть выполнен оптимально в смысле минимизации ошибки вычисления (4). В общем случае матрица управляемости может быть численно плохо обусловленной из-за многократного умножения матрицы А, но во многих случаях плохая обусловленность может быть исправлена специальными методами.
Метод матрицы управляемости (controllability matrix method) может быть использован для вычисления коэффициентов характеристического полинома многомерной системы, когда следующие два условия удовлетворены:
1) матрица А имеет общий вид;
2) вектор b не лежит в А-инвариантном подпространстве.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.