Управление движением запасных частей в ООО «Медведь АТЦ» дилер Фольксваген, страница 15

Для удобства расчетов вводятся относительные величины рассматриваемых стоимостных показателей  (в процентах), тем самым производится нормирование показателей:

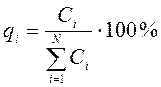_,                                          (3.19)

Величины  суммируются нарастающим итогом  и в зависимости от последующего способа определения номенклатурных групп представляются в виде графика. На оси ординат наносятся значения , на оси абсцисс – индексы , соответствующие присвоенным номерам позиций номенклатуры ЗПЧ. Точки с координатами () на графике соединяются плавной кривой , которая в общем случае является выпуклой. Затем проводится касательная  к кумулятивной кривой , параллельно прямой . Прямая  соответствует равномерному распределению затрат по всей номенклатуре, то есть характеризует долю определенной детали.

Абсцисса точки касания , округленная до ближайшего целого значения отделяет от всей номенклатуры деталей первую группу  (группа А), в которую входят детали с показателями . Соответственно ордината точки  -   указывает долю группы деталей в общем показателе .

Деление оставшейся номенклатуры деталей на группы производится аналогично вышеописанному. Соединим точку  с точкой  и проведем касательную к кривой , параллельную прямой . Абсцисса точки касания  делит оставшуюся номенклатуру деталей также на две группы : группу В и группу С.

          Доля оставшейся так называемой осредненной детали составит:

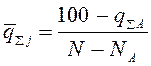,                                                 (3.20)

где      - число деталей (номенклатура) группы А.

Таким образом, в группу В попадают детали с показателем , подчиняющимся неравенству

Группировка номенклатуры по изложенному методу АВС – анализа позволяет проводить анализ удельных расходов (затрат) деталей и узлов на эксплуатационные нужды.

Характер изменения удельной стоимости по существующим нормам и, соответственно, по нормам на текущего ремонта и капитального ремонта достаточно близки между собой, что подтверждает правильность выбора перечня исследуемых деталей  поставленной задачи.

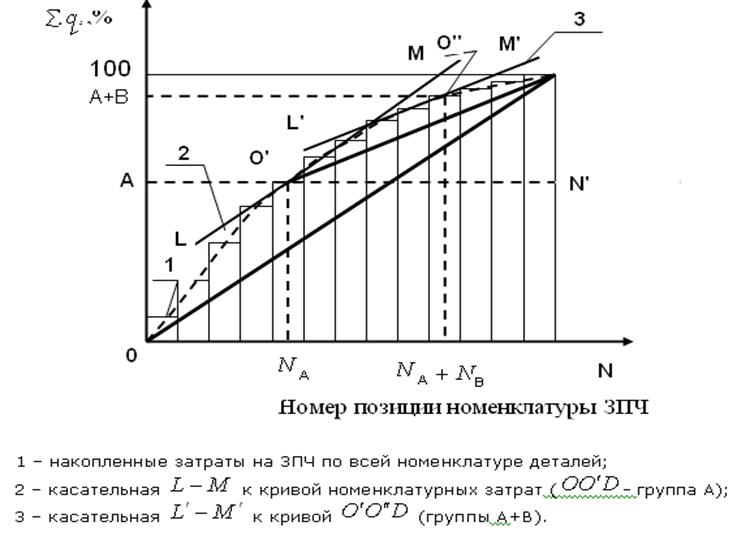
Рисунок 3.9 – Определение номенклатурных групп АВС

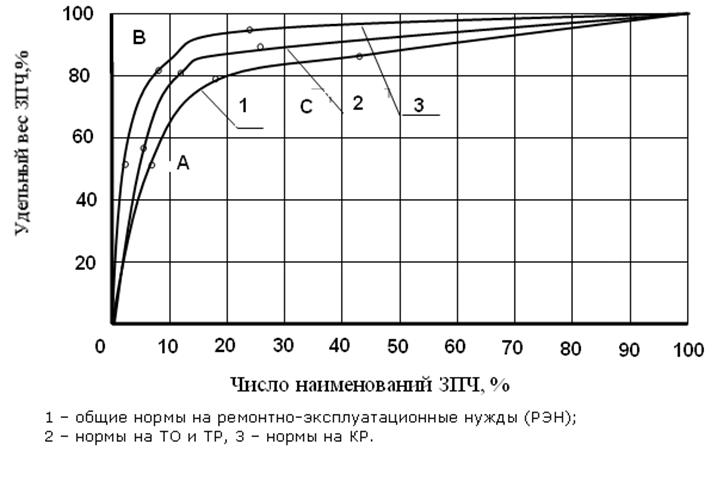
Рисунок 3.10 – Иллюстрация к АВС анализу

Вывод: Данный метод позволяет оптимизировать поступление ЗЧ по группам с экономической точки зрения, учитывая расход ЗЧ на статистических данных. 

11) Аналитический метод АВС анализа [14]

Для удобства расчетов число деталей N целесообразно нормировать в интервале 0 до 1 и ввести аргумент х.

Задается вид функциональной зависимости у =f(х, а_р), где а_р — коэффициенты. Коэффициенты а_р определяются с использованием метода наименьших  квадратов.

Для нелинейных зависимостей типа  и других выполняются необходимые преобразования для приведения к «нормальному» виду, т.е. к виду, позволяющему получить систему нормальных уравнений.

При определении коэффициентов а_р необходимо соблюдать начальные условия: первое, при х = О, у = 0; второе, при х = 1, у = 1. Это позволит сократить число уравнений для определения коэффициентов а_р.

Для определения координат точки О' воспользуемся теоремой Лангранжа, согласно которой:

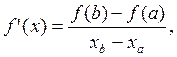                                           (3.21)

где   f '(х) — производная функция f(х) в точке касания;

f(b), f(a) — значения функции f(х)  в начальной и конечной точках.

Решив уравнение относительно х_а, тем самым определим абсциссу и далее переходим к номенклатуре по формуле, которая делит номенклатуру на две группы:

,                                                  (3.22)

Вводим новую систему координат, принимая за начало отчета абсциссу х_а и ординату у(х_А). В некоторых случаях для унификации расчета шкалы по осям могут быть вновь отнормированы. Таким образом, основное уравнение  записывается в виде:

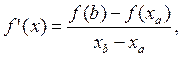                                          (3.23)

Полученные значения указывают координаты точки О' — границы группы А. Домножив Х_А на количество (номенклатуру) деталей данного узла ТУ, получим количественную оценку числа наименований деталей группы А. Определим координаты точки О" при подстановке Х_А, Y_Ав формулу.