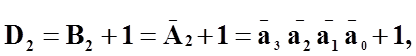Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 8

 

де число 1 додається шляхом двійкової арифметики.

       Код Грея,  який часто називається циклічним,  має ту особливість,  що при переході з одного десяткового числа до іншого сусіднього в ньому проходить зміна “0”  на “1”,  або навпаки,  тільки в одному розряді. Як видно з таблицi, код, представляємий двома, трьома або чотирма розрядами завжди створює циклiчну послiдовнiсть, тобто адекватну можливiсть переходу вiд старшого кодового значення числа до молодшого. Ця особливiсть дає можливiсть використовувати його при кодуваннi кутових перемiщень в перетворювачах кута повороту в цифровий код. Код Грея знаходить також широке використання в рiзних перетворювачах "аналог-код", де його властивiсть дає можливiсть звести до одиницi молодшого розряду   похибки   неоднозначностi   при   зчитуваннi   iнформацiї  [ .. ].

Для одержання коду Грея в літературі описані декілька різних прийомів. Один з них дозволяє будувати код Грея безпосередньо з двійкового, використовуючи слідуюче правило: -і-й біт коду Грея кодового слова встановлюється в нуль, якщо і-й і і+1-й біти відповідного двійкового коду однакові. В протилежному випадку біт і=1. В тому випадку, коли і+1-й біт виходить за рамки розрядності двійкового коду, то його значення приймається рівним нулю.

       При записi слiв двiйкового коду використовують шiстнадцяткове счислення,

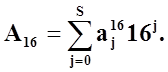                При його використаннi десяткові числа вiд 10 до 15 замiнюються вiдповiдно латинськими лiтерами A, B, C, D, E, F. Двiйковий i шiст-надцятковий коди легко взаємно переводяться. Для цього двiйкове слово будь-якої довжини розбивається на тетради, починаючи з молодшого розряду i вiдповiдно до табл.1.1 та вищезазначеними еквiвалентами лiтер та цифр записується його шiстнадцяткове представлення. Наприклад,  A₂ = 111011 = 00111011 = 3B₁₆ . В практицi використання цього коду, щоб не ставити   iндекс  коду,  пiсля  його  числового  значення  додають  букву h.

3B₁₆ = 3Bh.

        В задачах мiкропроцесорної та обчислювальної технiки часто з'являється необхiднiсть працювати з десятковими числами. Для цього використовують двiйкове перетворення кожної цифри окремо в вiдповiдностi  з  табл.  1.2.

         Наприклад, числу 937 вiдповiдає код 1001 0011 0111. Таке представ-лення називається двiйково-десятковим кодом, або кодом 8-4-2-1 у вiдповiдностi з ваговими коефiцiєнтами розрядiв. Але при виконаннi арифметичних операцiй з використанням двiйково-десяткового коду з'являються проблеми, пов'язанi з переносом з одного розряду до iншого. Для вирiшення цих проблем використовуються самодоповнюючi коди. До них вiдносяться код Айкена, ваговi коефiцiєнти розрядiв якого: 2-4-2-1, а такожкод "з надлишком 3". Код "з надлишком 3" одержується з двiйково-десяткового  шляхом  додавання  числа 3.

         Особливостi цих кодiв можна побачити з табл. 1.2.

                                                                                        Taбл. 1.2

Десяткове число	Двійково-десятковий код				Код Айкена 2-4-2-1				Код “з надлишком 3”
A10	a3	a2	a1	a0	h3	h2	h1	h0	c3	c2	c1	c0
0	0	0	0	0	0	0	0	0	0	0	1	1
1	0	0	0	1	0	0	0	1	0	1	0	0
2	0	0	1	0	0	0	1	0	0	1	0	1
3	0	0	1	1	0	0	1	1	0	1	1	0
4	0	1	0	0	0	1	0	0	0	1	1	1
5	0	1	0	1	1	0	1	1	1	0	0	0
6	0	1	1	0	1	1	0	0	1	0	0	1
7	0	1	1	1	1	1	0	1	1	0	1	0
8	1	0	0	0	1	1	1	0	1	0	1	1
9	1	0	0	1	1	1	1	1	1	1	0	0