fгр£ 1/2Т
Спрощена графічна ілюстра-ція теореми демонструється рис.1.8. Точність відтворення сигналу з імпульсної послі-довності тим вище, чим вище частота квантування відносно верхньої частоти спектру інформаційного сигналу.
Іншими словами дискре-тизація в часі не пов’язана з втратою інформації, якщо частота дискретизаціїfд =1/Tв два рази перевищує верхню частоту сигналу fв. Крок квантування T може бути як постійним, так і змінним в залежності від вимог, які ставляться при відновленні сигналу.
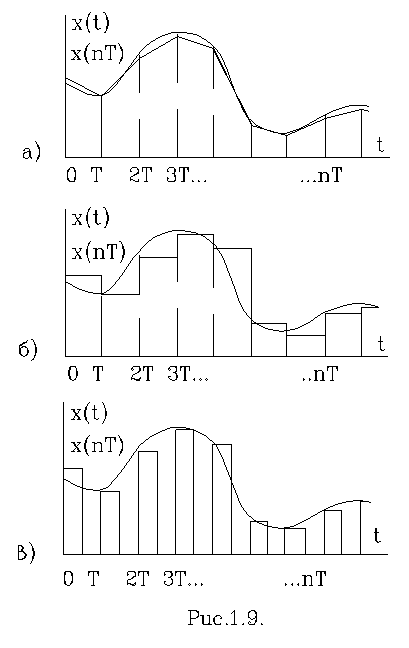
Дискретні значення функції x(nT) можуть використовуватись для відновлення сигналу. Знову ж таки на практиці використовується широка гамма методів відновлення сигналу з квантованованої послідовності d-імпульсів. Це може бути лінійна апроксимація (рис.1.9,а), ступінчата (рис. 1.9,б), або перетворення в імпульсні послідовності з заданими видами модуляції (рис.1.9,в).
1.1.3. Оцифровка аналогових сигналів.
Для використання сучасних засобів обробки сигналу поряд з дискретизацією в часі викорис-товується дискретизація по рівнях.
 Цей
спосіб дискретизації, який часто називають квантуванням по рівню, полягає в
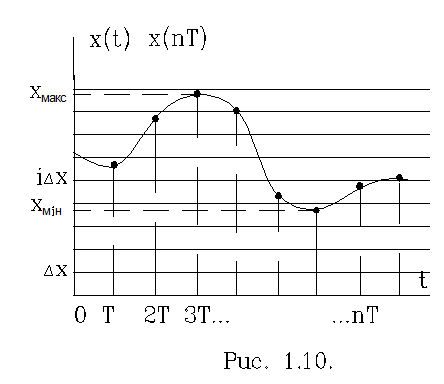
тому, що без-перервна вісь рівнів замінюється дискретною з кроком Dx. (рис 1-10). Фактично квантування по рівнях представляє собою
окру-глення значень x(nT) функції x(t) з заданою точністю. Квантування по рівню може бути як рівномірним, так
і нерівномірним. При рівно-мірному квантуванні кількість можливих рівнів m
Цей
спосіб дискретизації, який часто називають квантуванням по рівню, полягає в
тому, що без-перервна вісь рівнів замінюється дискретною з кроком Dx. (рис 1-10). Фактично квантування по рівнях представляє собою
окру-глення значень x(nT) функції x(t) з заданою точністю. Квантування по рівню може бути як рівномірним, так
і нерівномірним. При рівно-мірному квантуванні кількість можливих рівнів m
m=(хмакс-хмін)/Dх, (1. 9)
 де хмакс,
хмін - відповідно верхня і нижня межа зміни сигналу x(t).
де хмакс,
хмін - відповідно верхня і нижня межа зміни сигналу x(t).
Величина Dх визначає похибку, що має місце при заміні поточного значення x(t) його дискретним рівнем і*Dх = хі . Ця похибка, що знаходиться по формулі:
j(х)= х- хі
називається шумом квантуван-ня. Якщо при квантуванні по рівню будь-якому значенню змінної x(t), що попадає в інтервал хі+Dх/2, хі - Dх/2 присвоюється рівень хі , то похибка j(х)не буде превищувати половини шагу квантування, тобто:
?j(х)?макс = Dх/2.
В теорії сигналів широко використовується імовірносна оцінка шумів квантування.
Важливою характеристикою будь-якого сигналу являється його інформативність. Тому необхідно мати кількісну характеристику інформації.
Для її визначення розглянемо спрощену дискретну модель реального сигналу, заданого на інтервалі часу Тс , і квантованого в часі і по рівню.
Використовуючи умови теореми Котельникова приблизна кількість дискрет, що визначають функцію [ ]:
n = Tc /T =2fмакс *Тс ,
де fмакс - максимальна частота в спектрі сигналу.
Кількість можливих рівнів квантування m визначається формулою (1. 9).
Так як в кожний дискретний момент часу сигнал може приймати одне зm можливих значень, то за час Тс кількість можливих комбінацій сигналу.
Сс = mn
Тобто число Cc дає комбінаторну оцінку кількості інформації, що вміщується в дискретному сигналі. Недолік використання Cc в якості міри інформації полягає в нелінійній його залежності від величини n , тобто від тривалості інтервалу Tc. Тому за міру кількості інформації використовується логарифмічне перетворення від Cc, тобто:
![]() I = log b Cc =n log b m,
I = log b Cc =n log b m,
в якому маємо лінійну залежність між вказаними параметрами. Вибір параметра b впливає лише на розмірність, тобто на одиницю виміру кількості інформації. Найчастіше приймають b=2, при цьому I вимірюється в бітах (binarydigit). Один біт – це найменша кількість інформації, що відповідає одному з рівноможливих повідомлень (так-ні ; ввімкнути-вимкнути, тощо). Він може представлятись лише числами “1”, ”0”, послідовність яких буде давати більш детальну характеристику повідомлень. Повідомлення , в якому міститься набір з декількох бітів називається словом. Слово з 8 біт називається байтом. Якщо, наприклад, допустити, що кількість рівнів квантуванняm описується словом в один байт, то це значить, що весь діапазон рівнів хмакс – хмін розбивається на m =28 = 256 кроків, функція буде визначатись з похибкою ?j(х)?= (256*2)-1 і в кожний дискретний момент часу може передаватися повідомлення про одне з її 256 можливих значень.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.