 При
використанні карт Капрно для функцій з більшою кількістю логічних змінних
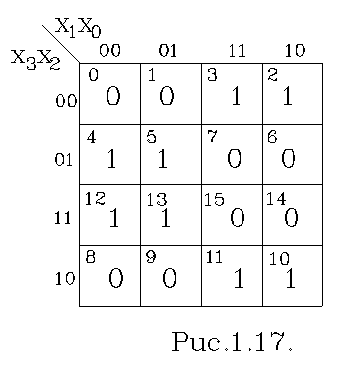
зростає кількість клітин в Карті відповідно з формулою N=2n. Для n=4 карта Карно приведена на рис. 1.17.
Функція, що приведена в карті в скороченій аналітичній формі має вигляд:
При
використанні карт Капрно для функцій з більшою кількістю логічних змінних
зростає кількість клітин в Карті відповідно з формулою N=2n. Для n=4 карта Карно приведена на рис. 1.17.
Функція, що приведена в карті в скороченій аналітичній формі має вигляд:
у = å 2, 3, 4, 5, 10, 11, 12, 13.
З карти Карно также легко перейти до табличної форми запису. Якщо задана функція неповністю визначена, то подібно до таблиці, в відповідних клітинах записується знак невизначе-ності, що дає можливість повністю відобразити всі властивості функції.
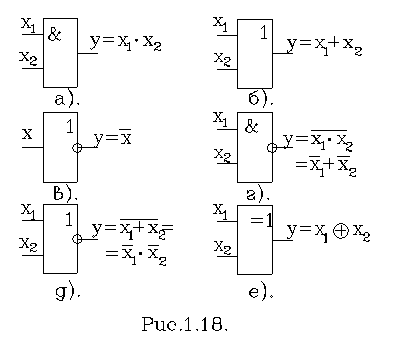 Графічна
інтерпретація грунтується на використанні умовних позначень логічних функцій,
які являються стандартними. На рис. 1.18. приведені умовні позначення,
характерні для стандартів, прийнятих в СНД. Використання приведених умов-них
позначень дає можливість бу-дувати складні логічні схеми, принципові схеми
електроних при-строїв, а також використовувати в спеціальних програмах для
розробки друкованих плат. Приведені логічні елементи реально виготовляються в
багатьох серіях мікросхем.
Графічна
інтерпретація грунтується на використанні умовних позначень логічних функцій,
які являються стандартними. На рис. 1.18. приведені умовні позначення,
характерні для стандартів, прийнятих в СНД. Використання приведених умов-них
позначень дає можливість бу-дувати складні логічні схеми, принципові схеми
електроних при-строїв, а також використовувати в спеціальних програмах для
розробки друкованих плат. Приведені логічні елементи реально виготовляються в
багатьох серіях мікросхем.
Ще одною формою представлення логічних функцій являються часові діаграми. Вони відображають часові співвідно-шення між вхідними логічними змінними, представленими в вигляді часових діаграм, і вихідною функцією (Рис.1.20). Часові діаграми зображаються з врахуванням фронтів імпульсних послідовностей з відображенням моментів початку перехіднихї процесів і часто мають
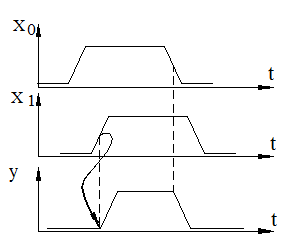
 Рис.1.19
Рис.1.20
Рис.1.19
Рис.1.20
допоміжні вказівні стрілки, які уточнюють хід перехідних процесів в схемі.
На рис. 1.20. приводиться приклад часових діаграм для логічної схеми, що реалізує операцію цифрового компаратора, зображеної на рис.1.19. В розглядаємому випадку приводиться лише вхідні сигналі і вихідні. При визначені інтервалів часових затримок, тривалості перехідних процесів приводиться більша деталізація часових діаграм.
1.6.4 Мінімізація логічних функцій.
Логічні функції реалізуються з допомогою мікросхем, орієнтованих на виконання тих чи інших операцій. Мікросхеми загального використання здебільшого можуть реалізовувати декілька простих одиночних операцій. По цій причині справедливо стверджувати, що чим простіше аналітична форма запису логічної функції, тим менше використовується логічних елементів і, як результат, тим менше мікросхем необхідно для її реалізації. Складність логічних функцій визначається кількістю логічних зміних , що входять до їх складу в прямому і інверсному виді і кількстю простих логічних операцій над ними. Люба логічна функція може бути записана різними аналітичними виразами різної степені складності. Серед них можна знайти такі, які містять мінімальну кількість логічних зміних і операцій над ними. Задача знаходження таких аналітичних виразів називається мінімізацією логічних функцій. Звідси витікає, що мініізація логічної функції- це заміна логічної функції, що представлена у вигляді логічної суми мінтермів або логічного добутку макстермів іншою логічною функцією зх мінімальною кількістю логічних змінних та операцій над ними.
Задача мінімізації- це задача неоднозначна і різними шляхами можна отримати різні вирази мінімізованої функції, що відрізняються кількістю змінних і операцій над ними.
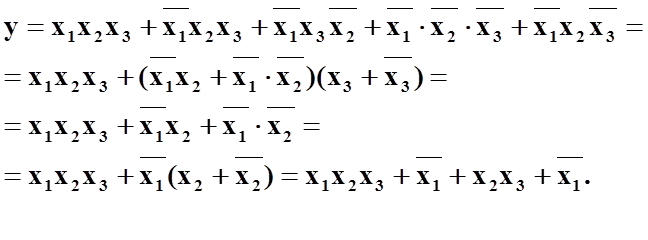 |
Одержана ДНФ має мінімальну складність.
Фактично операція мінімізації має на увазі ту умову, що мінімізуєма логічна функція Y містить в собі логічну функцію Y’, примчому для будь-якої вхідної комбінації змінних Y. При яких вона приймає істинні значення, функція Y’ теж буде приймати істинні значення. Тобто функція Y’ розміщується на тій жемножині логічних змінних, що і функція Y. Звідси витікає можливість переходу до графічної інтерпретації задачі мінімізації з використанням карт Карно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.