Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 16

                                                                                         Табл. 1.4

Аксіоми (тотожністі)
	0 · х = 0
	1 + х = 1
	0 + х = х
	x· х = х
	х +х=х
	х · =0
	х +=1
	= х
Закони комутативності	х1 + х2 = х2 + х1
	х1 · х2 = х2 ·  х1
Закони асоціативності	х1 + х2 + х3 = х1  +(х2 + х3)
	х1·х2·х3 = х1·(х2 · х3)
Закони дистрибутивності	х1·(х2+ х3)=х1·х2+х1· х3
	х1+х2·х3=(х1+х2) · (х1+х3)
Закони інверсії (теорема де-
Моргана)(принцип подвійності)
Закони поглинання	х1+х1·х2=х1
	х1· (х1+х2)=х1

Використовуючи наведені в табл. 1.4 закони та тотожністі, які використовуються при перетворенні логічних функцій можна створювати нові.  Наприклад:

(х₁+х₂) · (х₁+х₃)=х₁+х₂·х₃;

х₁· (+х₂)=х₁·х₂;

х₁·х₂=х₁+х₂

  (В подальшому крапки, що відображають операцію логічного перемноження  в формулах приводити не будемо).

1.6.3 Способи задання логічних функцій.

Існує чотири способи задання або запису логічних функцій - аналітичний, табличний, за допомогою карт Карно  та графічний.

Аналітично логічна функція може бути записана різними комбінаціями кон¢юнкцій та диз¢юнкцій логічних змінних. Звичайно логічні функції записуються або у вигляді суми добутків логічних змінних (диз¢юнкція кон¢юнкцій) або у вигляді логічного добутку їх сум (кон¢юнкція диз¢юнкцій). Наведення функції у вигляді диз¢юнкції кон¢юнкцій називають диз¢юнктивною нормальною формою (ДНФ):

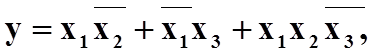а запис у вигляді кон¢юнкції диз¢юнкцій - відповідно кон¢юнктивною нормальною формою (КНФ):

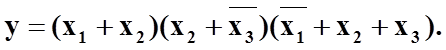Інверсія будь-якої функції у відповідності з теоремою де Моргана будь-якої функції наведеній в одній формі призводить до заміни запису на іншу форму.

Наприклад інверсія функції

представляється у вигляді:

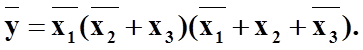Будь-яка логічна функція, задана в аналітичній формі може бути перетворена на ДНФ або КНФ за допомогою тотожностей та законів алгебри логіки. При цьому для одній і тєї ж функції може існувати декілька рівнозначних диз¢юнктивних та кон¢юнктивних нормаль­них форм.

В той же час існує лише один вид ДНФ та КНФ, в яких функція може бути записана єдиним чином. Такі форми називаються досконалими (ДДНФ, ДКНФ). Вони характеризу­ються тим, що в ДДНФ кожна кон¢юнкція, а в ДКНФ кожна диз¢юнкція містять всі логічні змінні даної функції, з інверсіями або без них.

Прикладами ДДНФ та ДКНФ запису являються функції чотирьох змінних

                                          

                                1010               0110                   1011

Так як кожна кон¢юнкція функції, що наведена у ДДНФ визначає її істинне значення, відповідаюче “1”, то такі кон¢юнкції називаються конституєнтами одиниці (мінтермами). Аналогічно диз¢юнкції функції, що наведені у ДКНФ називаються конституєнтами нуля (макстермами).

Якщо замінити логічні змінні та їх заперечення одиницями та нулями, то кожна кон¢юнкція буде представляти собою двійкове число.

Це дозволяє, наприклад вище наведену функцію у₁ представити у вигляді:

у₁=å 10, 6, 11

Така форма називається досконалою  скороченою аналітичною формрю, або канонічною сумою.

Аналогічно, функцію можна зобразити і в вигляді макстермів. Така форма запису називається канонічним добутком. Наприклад:

Легко бачити можливість конвертації  в представленні функції в вигляді макстермів та мінтермів, оскільки кожна з них доповнює функцію до повного переботу логічних змінних. Як приклади можемо записати:

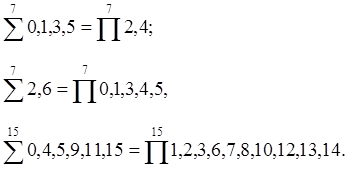
Досконала диз¢юнктивна нормальна форма запису дозволяє легко перейти до інших форм запису – табличної  та  в вигляді карт Карно.