Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 26

е_пi =L_шi *I_bi/t_фр,

де t_фр тривалість фронту імпульсів. На мал 1.22,б приводиться схема заміщення для розрахунку величини е_пi. Максимальна величина   перешкоди   буде   при   синхронній   комутації  всіх  вузлів[  ]

                                       е_п.макс=L_шi*(I_bi/t_фр)*i*(i-1).

   Розглянемо один з прикладів появи перешкод такого типу-перешкод, обумовлених затримками в перемиканні логічних елементів.

При розгляді роботи логічних функцій використовувались умови, що логічні елементи премикаються миттєво, не маючи часових затримок і стан виходу логічної функції оцінювався в статичному режимі, тобто, коли вхідні сигнали не змінюються. Але реальні логічні елементи мають часові затримки при перемиканні, величини яких залежать від різних факторів, тому і значення логічної функції при зміні значень її аргументів також може бути непередбаченим.

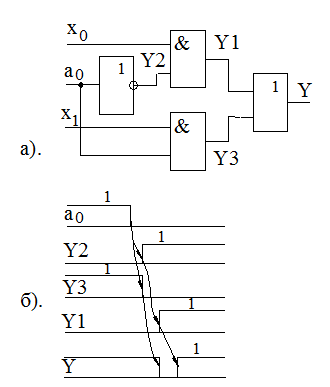Осільки логічні елементи мають реальні часові затримки при перемиканні, то під час перемикання  кола передачі інформаційних сигналів можуть відрізнятись від тих, що мали місце в статичних режимах. Це може приводити до непередбачених ситуацій, тому логічні схеми слід розглядати і в динамічних режимах перемикання. Одною з особливостей поведінки логічних схем в динаміці являється поява короткочасних імпульсних перешкод. Тому пректантам електронних цифрових схем необхідно передбачати можливість появи таких ситуацій і забезпечувати проектування з уомви неможливості появи імпульсних перешкод, даже в самих тяжкиж впадках.

Будь –яка комбінаційна схема повинна аналізуватись на можливість появи перешкод. Оле добре спроектовані синхронні цифрові схеми здебульшого структуровані так, що забезпечують неможливість появи подібних перешкод. В синхронних системах всі входи кобінаційних кіл змінюються одночасно, а сигнали на виходах появляються лише після установлення перехідних процесів. Аналіз на можливість появи перешкод необхідно прововдити лише для асинхронних цифрових схем, а також для схем з зворотніми зв’язками, які розглядаються, починаючи з розділу 4.

 Статичні перешкоди можуть бути двох типів- поява короткочасного імпульса нульового рівня при наявності сигналу одиничного рівня на виході і навпаки – поява короткочасного імпульса одиничного рівня при наявності сигналу нульового рівня на виході. Прикладом створення перешкоди першого типу явуляється схема, що приведена на рис.  а. Це схема мультиплексора, що забезпечує передачу на вихід значення  одного з інформаційних входів х₀, х₁ який вибирається адресним сигналом а₀. Допустимо, що сигнали х₀ і х₁  мають одиничні значення, а адресний сигнал а₀ змінюється з 1 в 0. (рис.   б). Так як зміна сигналів а₀ і Y2 відбуваються в різні інтервали часу, то нескладний аналіз часових діаграм і роботи схеми показує, що між моментом зникнення одиниці х₁ на виході Y і моментом появи там же одиниці х₀ має місце корткочасна пауза, яка являється імпульсною перешкодою нульового рівня.

Імпульсні перешкоди одиничного рівня можуть появитись на виході схеми в тих випадках, коли має місце перемикання одного сигналу низького рівня на інший які подаються на вихід схеми через логічні комутатори.

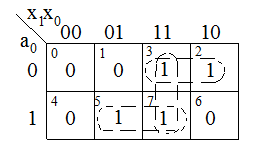
Визначити можливість  появи статичних перешкод в проектуємій логічній схемі можливо з допомогою карт Карно.  Проаналізуємо карту Карно для для розглянутої схеми. (рис.   ) Зробивши обєднання клітинок 2, 3 і 5,7 отримуємо логічну функцію

Але в той же час  з такого обєднання можна зробити висновок, що неодночасна зміна сигналів, що забезпечують логічні одиниці в клітинах 3 і 7 приведе до появи перешкоди. Звідси також витікає і реальний практичний варіант усунення вказаного недоліку розглядаємої схеми. Він полягає в тому, що необхідно допоміжно обєднанти кілтини 2 і 7. При цьому логічна схема примйме вигляд:

а на схемі добавиться один допоміжний логічний елемент 2І, який виключе можливість появи перешкоди.