Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 2

      На рис. 1.2. зображений типовий одиночий імпульс та приведені у взаємозв’язку його амплітудні та часові параметри. До амплітудних відносяться: U_max – максимальне значення параметра імпульса (його 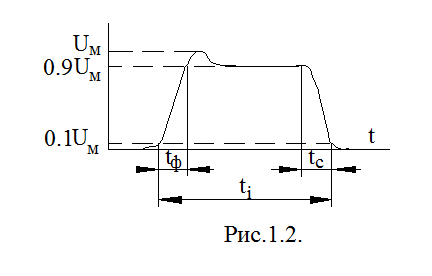амплітуда); ∆U – спад вершини. До часових t_φ, t_c – протяжність  фронту  та  спаду  імпульса;  t_i– протяжність  імпульса.

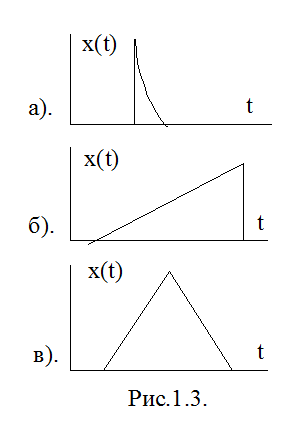Параметри імпульсу можуть змінюватись в широких межах і, відповідно, одиночні імпульси можуть мати різну форму. На рис. 1.3. а, б, в зображені, відповідно,  експоненціальний,  пиловидний  та  трикутний  імпульси.

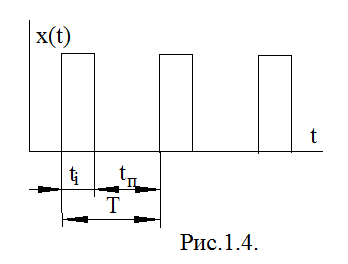
          Імпульсна послідовність харатеризу-ється наявністю пауз між одиночними ім-пульсами. Під паузою t_псприймається нульовий рівень напруги чи струму, або такий рівень, який прирівнюється до нульового. (рис. 1.4.) Якщо протяжність періодів в послідовності не змінюється, то говорять про періодичну послідовність, яка характеризується періодом T=t_і+t_п, коефіці-єнтом заповнення s=t_i/T та скважністю q=s^-1

         В  теоретичних  дослідженнях  часто  використовуються  ідеалізації  імпульсів.

         Перша  з  них  –  це  функція  включен-ня,  або  функція  Хевісайда. В загальному  випадку функція включення, зміщена віднос-но початку осі координат на величи-ну  t₀, записується в вигляді ( рис.1.5.)

               ì 0,     при  t < t₀

  s(t-t₀) =í 0.5,  при  t = t₀              (1.4)   

               î 1,     при  t > t₀

       В теорії сигналів фунції включення  дуже широко використовуються для опису розривних та імпульсних сигналів. Імпульсний сигнал прямокутної форми, наприклад, записується так:

                (1.5)

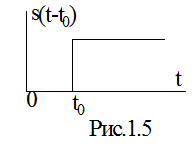Особливість  цього імпульсу  полягає в тому, що при будь-якій величині параметру ξ його площа: 

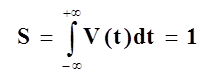
                                                  (1.6)

залишається незмінною при ξ→0

         Межа фунції при ξ→0 носить  назву дельта-фунції,  або  фунції  Дірака:

                                                   (1.7.)                                                                                                             

          Фунція Дірака відповідає особливості  (1.6.). Другою особливістю явялється те, що її розмірність відповідає розмірності частоти.

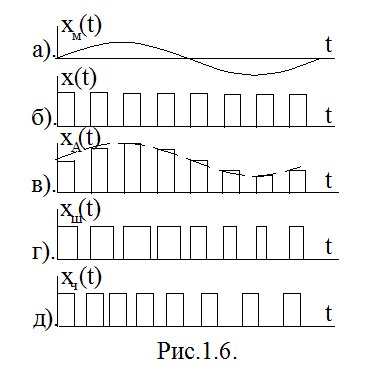
  Для передачі інформації імпульсною послідовністю вона модулюється по аналогії з синусоїдою. В залежності від модулюємого параметру розрізняють амплітудно-імпульсну модуляцію (АІМ), широтно-імпульсну (ШІМ), часово-імпульсну, яка поділяється на фазо-імпульсну модуляіцю (ФІМ) та частотно-імпульсну (ЧІМ). Рис.1.6. ілюструє особливості модуляції імпульсної послідовності x(t) (рис.1.6.б) фунцією x_μ(t)  (1.6.а) відповідно при АІМ  (x_A(t), рис.1.6.в ),  ШІМ  (x_ш(t),  рис.1.6, г),  ЧІМ (x_ч(t),  мал. 1.6, д).   

          Використання процесів модуляції неможливо без наявності зворотніх процесів – виділення інформаційного сигналу з модульованого. Такі зворотні процеси  називаються  демодуляцією,  або  детектуванням.

          В практиці передачі інформації часто використовуються операції перетворення  непреривного  сигналу  в  імпульсний  та  навпаки.

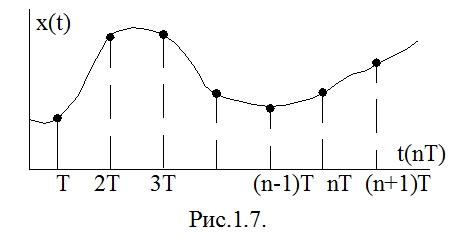
         Загальновизнано, що вихідним сигналом при перетворенні являється аналоговий. Для перетворення його в імпульсну або в іншу дискретну форму необхідно здійснити дискретизацію (квантування) цього сигналу як в часі, так  і  по  рівню.

         При квантуванні в часі непреривний час осі t замінюється на дискретний з кроком (періодом квантування Т) (рис..1.7).

 В залежності від способів реалізації квантування в часі створюєма імпульсна послідовність може мати різне математичне описання. При перетворенні

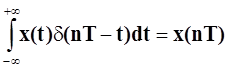інформаційних сигналів для цього використовують функцію (1.7), завдяки особливості згортки цієї функції:

                                             (1.8)

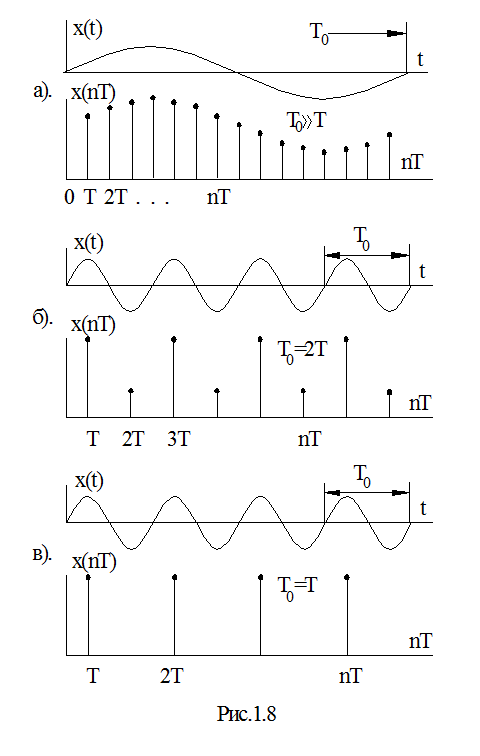
        Ця особливість відо-бражає фільтруючу власти-вість дельта-функції і заклю-чається в тому, що після виконання операцій множен-ня та інтегрування, функція x(t) буде визначеною лише в точках квантування в часі nТ. (Іншими словами, функція визначається з точністю до кроку кванту-вання nТ). Величина кроку квантування в часі вибира-ється в відповідності з необ-хідною точністю відтворення непреривного сигналу. В відповідності з теоремою ак. Котельникова максимальна  частота, яка може бути відновлена з сигналу, пред-ставленому в  вигляді диск-ретної послідовності, не може перевищувати   величину