Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 22

В загальному плані, якщо ми маємо шину передачі даних шириною в n- біт, то вона може забезпечувати передачу  2ⁿ кодових слів.  Для того, щоб виявити одиночну помилку, необхідно мати лише 1 допоміжний біт, так як це дає можливість  в n- вимірному кубі мати мінімальну відстані – 2. На практиці такий біт називається бітом парності, що пов'язано з особливостямит схемотехніки.

1.7.3. Коди, що коригують одиночні помилки і виявляютьвелику кількість помилок. 

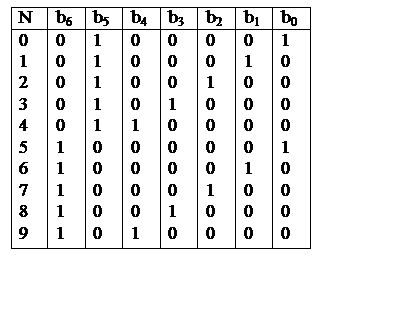Використання більшої кількості біт в кодових словах дає можливість зробити мінімальну відстань більшу ніж 2, що відкриває можливість не тільки виявляти, а і виконувати корекцію спотворених кодових слів. Прикладом коду, який доє можливість легко виявити помилку в передачі являється  подвійно пятирічний код. Його значення приведені в таблиці   .  Старші два біти b₆b₅  розділяють всі коди на дві групи: молодших десяткових чисел 0-4 , які кодуються однаково b₆b₅ =01;

старших десяткових чисел 5-9, які мають код  b₆b₅ =10.

Молодші 5 розрядів формують коди 1 з 5 . Як видно з таблиці поява помилки в будь-якому біті такого коду  легко може бути виявлена а інформація буде признана помилковою.

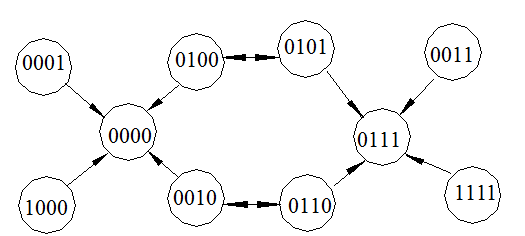Розглянемо тепер, як можна використовувати коди для корекції одиночних помилок, або виявлення великої їх кількості. . Допустимо, що код має мінімальну відстань 3. Рис. .. показує фрагмент n-вимірного куба для такого коду з кодовими словами 0000 і 0111. При відстані 3 маємо 3 біта різниці між двома сусідніми вершинами куба. Допустимо, тепер, що передається інформація і при її передачі має місце помилка в одному біті. Якщо передається кодове слово 0000, то з помилкою можуть біти отримані слова, які на рис.   оточують вказане кодове слово. В такому випадку при появі одиночної помилки появляються некодові слова, які відрізняються від кодового слова лише на один біт. Вони не тільки легко можуть бути виявлені а і виправлені, що відображено стрілками на рис.   . Аналогічна картина має місце і стосовно другого кодового слова. Наприклад, створення некодового слова 0101 з більшою імовірністю відповідає кодовому слову 0111, ніж 0000.

Таким чином при прийомі інформації необхідно приймати рішення, яке з кодових слів дійсно отримане. Такуе рішення являється операцією декодування з виправленням помилок, а відповідні апаратні засоби- декодери з виправленням помилок. Код, що використовуються для виправлення помилок при передачі інформації, називаються коригуючими.

В загальному плані, якщо код має відстань 2b+1, то він може бути використаним для корекції помилок, що впливають на b біт. Якщо ж коди мають мінімальну відстань 2b+c+1, то вони можуть бути використані для корекції помилок в b біт і вявляти помилки в c бітах.

Прикладом такого коду являється код Хемінга. Він може бути створний для будь-якого  цілого числа і, яке визначає  код довжиною 2^і-1 біт з і розрядів парності і 2^і-1 –і інформаційних розрядів з відстанню між кодовими словами –3.

Положення кожного розряду слова коду Хемінга нумерується від 1 до 2^і-1. Будь-який розряд з номером розміщення в слові, кратний 2 являється бітом парності, решта- інформаційні. Кожен біт парності об'єднаний в групу з підконтрольними йому інформаційними бітами. Таке об'єднання зроблено в табл.

                                                                                      Табл.