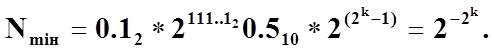Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 12

                                                                                                                                                                                                                                                                                                                                                 (1.15)

         Максимальне число будемо мати при максимальному значенні мантиси

(0.111…1)₂ максимальному позитивному порядку (111…1₂)= 2^k-1, тобто

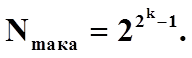                                               (1.16)

Діапазон D представляємих в нормальній формі чисел, як витікає з формул (1.15) та (1.16) визначається лише числом k. Для k=6, наприклад,  знаходимо

         Точність запису числа задається кількістю розрядівm мантиси. Якщо кількість розрядів числа перевершує відведену під мантису кількість розрядів, то число округляється до необхідної довжини. Правило округлення двійкових чисел в цьому випадку слідуюче: якщо старший розряд в частині слова, що відкидається являється одиницею, то до молодшого розряду мантиси додається одиниця. При такому округленні абсолютна похибка e зображення мантиси не перевершує половини вагового коефіцієнта молодшого розряду зберігаємої мантиси, тобто:

                                                          e < 2^-m/2

          Так як при нормальній формі запису мантиса не може бути меншою 0.5, то відносна похибка:

                                                         h£ 2Ô[ 2^-m

          При  m=24,  маємо:

                                                       h[ 2^-24 » 10^-7.2.

          В сучасних цифрових системах для зображення чисел з плаваючою комою використовується строчка довжиною чотири байти. При цьому 23 розряди задають мантису, а 7 величину порядка. Діапазон зображаємих чисел  складає  від  ± 2¹²⁷  до ± 2^-127

          Використання чисел з плаваючою комою суттєво розширює і спрощує зображення чисел, але виконання операцій над такими числами складніше, ніж над числами з фіксованою комою.

1.5 Виконання арифметичних операцій.

    Основною операцією, яка використовується в цифрових системах при виконанні різних обчислень являється операція алгебраїчного додавання. Вона виконується на основі правил виконання операцій в десятковій системі зображення  чисел, які для однорозрядних чисел мають слідуючу реалізацію:

     0          1         0         1

   +          +         +         +

     0          0         1         1 

   ___     ____   ____   ____

     0    ;     1    ;   1    ;   10  ; 

Перенос в старший розряд виконується тоді , коли в одному розряді обох складових є одиниці . Операція знаходження суми в багаторозрядних числах виконується послідовно, починаючи з молодшого розряду. В зв’язку з цим, починаючи з другого розряду, виконується складання трьох цифр, двох   розрядних   складових  і   перенос  з  молодшого  розряду.      

   Приклад:   скласти  два  позитивних  числа  А₂=1001₂;  B₂=1101₂.

        А₂ =   1 0 0 1 =   9₁₀

        +

        В₂ =    1 1 0 1 = 13₁₀

 ____________________  

(А+В)₂ = 1 0  1 1 0 = 22 

Операція віднімання виконується в цифрових схемах за допомогою операції  додавання,  зображуючи  від’ємник  в  допоміжному  коді.

         Приклад.  Знайти суму двох чисел N₁₀ =854₁₀  і  K₁₀ = -387₁₀ з використанням  допоміжногого  коду :

          Рішення: При виконанні вказаної операції в десятковій системі зображення необхідно для числа В₁₀ найти відповідний допоміжний код. Він знаходиться за тими ж правилами, що і в двійковій системі. Зворотній код числа знаходиться як доповнення до дев’ятки цифри кожного розряду. Для числа K₁₀ = 387 зворотній код В = 612. Позначення знакових розрядів – рискою  над  цифрою  розряду.

         Допоміжний код

 D = В + 1=612 + 1=613

Виконаємо  операцію  додавання :

 

        А + D =  0854 + 1613 =10467 = 467.

         Перенос,  що  з’являється зі знакового розряду, відкидається.

         Таким же шляхом виконується операція віднімання в двійковій системі зображення чисел.