Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 17

В табл. 1.5. наведені функції у₁ - у₅ двох змінних х₀  та х_1. Табличний спосіб полягає в тому, що функція задається у вигляді таблиці відповідності (таблиці істинності станів). В таблицю вписують всі можливі комбінації аргументів в порядку зростання їх індексів та кожній комбінації установлюється значення функції.Кількість всіх можливих сполук аргументів, а, отже, і                                                           кількість значень функції дорівнює 2ⁿ, де  n – кількість логічних змінних. З табличної форми запису легко перейти до аналітичної, використовуючи досконалу дізюнктивну форму запису логічних функцій. Для цього функція записується як дізюнкція конституєнт одиниці. Наприклад функцію у₃  з табл.1.5можемо записати в вигляді:

Ця функція може бути записана і з використанням нульових  її значень

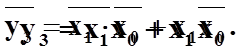Використовуючи властивість подвійної інверсії легко встановити тотожність обох форм запису.

Іноді функція являється неповністю визначеною. В табл.1.5 приводиться форма запису функції у₁, яка невизначена при х₁ =х₀ =1 При переході до аналітичної форми запису вона повинна бути довизначена.

Функції двох змінних займають в булевій алгебрі особливе місце. Для двох змінних кількість булевих функцій дорівнює 16. Ці функції називаються елементарними і складають максимальний набір функцій двох змінних. В табл.1.6 наведені всі елементарні функції двох змінних.

                                                                                                                                           Табл.1.6

N	х 0	0	1	0	1	Назва функції	Позначення
	х 1	0	0	1	1
0		0	0	0	0	Константа нуль	0
1		0	0	0	1	Кон¢юнкція, (І)
2		0	0	1	0	Заборона по х0
3		0	0	1	1	Змінна х1
4		0	1	0	0	Заборона по х1
5		0	1	0	1	Змінна х0	х0
6		0	1	1	0	Викл. АБО, сума по mod 2	х1Å х0
7		0	1	1	1	Диз¢юнкція, (АБО)	х1+х0
8		1	0	0	0	АБО - НІ, функція Пірса
9		1	0	0	1	Рівнозначність, еквівалентність	х1ºх0
10		1	0	1	0	Заперечення х0
11		1	0	1	1	Імпликація по х0	х0®х1
12		1	1	0	0	Запречення по х1
13		1	1	0	1	Імплікація по х1	х1®х0
14		1	1	1	0	Функція Шеффера І – НІ
15		1	1	1	1	Константа 1	1