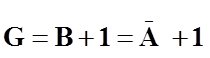 |
|
a3 |
a2 |
a1 |
a0 |
Знак і величина |
Прямий і зворотній |
Прямий і допоміжний |
|
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 |
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 |
+0 1 2 3 4 5 6 7 - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 |
+0 1 2 3 4 5 6 7 - 7 - 6 - 5 - 4 - 3 - 2 - 1 - 0 |
+0 1 2 3 4 5 6 7 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 |
На рис. 1.11 приведена графічна інтерпретація зображення позитивних і негативних чисел відносно нуля з вико-ристанням прямого та допоміжного кодів. Як буде зрозуміло пізніше, така форма представлення десяткових чисел суттєво спрощує виконання арифметичних операцій.
Тепер пояснимо суть запису чисел з фіксованою комою. Будь-яке число в циф-рових системах зберігається в спеціаль-них пристроях пам’яті, кожна строчка якого складаються з фіксованої кіль-кості елементів. Кома, що відділяє в числі цілу частину від дробної займає в строчці пам’яті фіксоване положення – перед старшим розрядом або після молодшого.
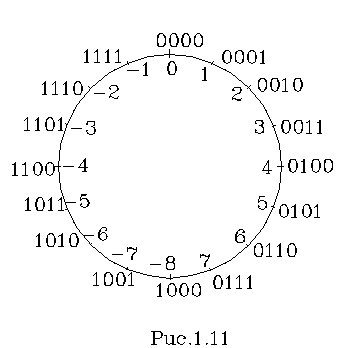 В першому
випадку абсолютне значення числа менше одиниці, напри-клад –0.1101012 . Якщо строчка пам’яті призначена для
десяти розрядів, то число в ньому запишеться так, як показано на рис.
1.12, де крайній лівий розряд відображає знак числа, а решта – розряди
модуля.
В першому
випадку абсолютне значення числа менше одиниці, напри-клад –0.1101012 . Якщо строчка пам’яті призначена для
десяти розрядів, то число в ньому запишеться так, як показано на рис.
1.12, де крайній лівий розряд відображає знак числа, а решта – розряди
модуля.
 Вільні молодші
розряди заповнюються нулями. Так як в розглядаємому випадку в строчці пам’яті передбачається запис лише дробної частини числа, то і результати
всіх операцій повинні бути з абсолютним значенням менше одиниці. Виконання цієї
умови забезпечується вибором відповідних масштабних коеффіціентів, на які
домножуються вихідні дані. Якщо масштабний коеффіцієнт вибраний невірно, то
може з’явитись переповнення розрядів і поява цілої частини, що приведе до її
втрати, так як в розрядній сітці не передбачена її поява. Все це приведе до
похибки в результаті, що є недоліком такого способу. В другому випадку , коли кома фіксується після молодшого розряду, то
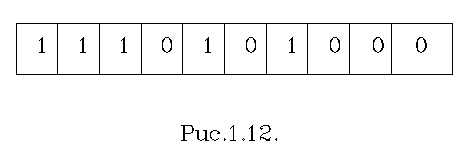
маємо справу з цілими числами. Тоді, наприклад, число 100112 в
строчці пам’яті розміщується в відповідності з рис. 1.13, де лівий розряд
знаковий, а слідуючі за ним справа вільні розряди заповнюються нулями. В цьому
випадку величина модуля є обмеженою довжиною строчки пам’яті.
Вільні молодші
розряди заповнюються нулями. Так як в розглядаємому випадку в строчці пам’яті передбачається запис лише дробної частини числа, то і результати
всіх операцій повинні бути з абсолютним значенням менше одиниці. Виконання цієї
умови забезпечується вибором відповідних масштабних коеффіціентів, на які
домножуються вихідні дані. Якщо масштабний коеффіцієнт вибраний невірно, то
може з’явитись переповнення розрядів і поява цілої частини, що приведе до її
втрати, так як в розрядній сітці не передбачена її поява. Все це приведе до
похибки в результаті, що є недоліком такого способу. В другому випадку , коли кома фіксується після молодшого розряду, то
маємо справу з цілими числами. Тоді, наприклад, число 100112 в
строчці пам’яті розміщується в відповідності з рис. 1.13, де лівий розряд
знаковий, а слідуючі за ним справа вільні розряди заповнюються нулями. В цьому
випадку величина модуля є обмеженою довжиною строчки пам’яті.
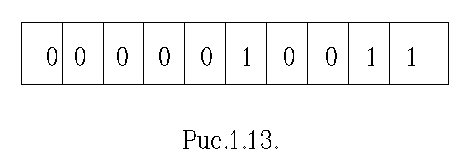 Числа з
плаваючою комою передбачають зображення числа з використанням ман-тиси, що
домножається на основу системи числення в степені, задаваємій порядком.
Наприклад, число 200 записується у вигляді 0,2×103, а
число 0,000312 = 0,312×10-3. Відповідно записуються і двійкові числа. Mантиса і
порядок зображаються в двійковому коді, а основою є двійка. Наприклад, число
0,111×210
= 11.10 в десятковій системі зображається як 0,875×22 = 3,5. В
строчці пам’яті такі числа зберігаються у вигляді двох груп цифр: перша
група, мантиса, визначає саме число, друга - порядок, - місце коми
в числі (рис.1.14).
Числа з
плаваючою комою передбачають зображення числа з використанням ман-тиси, що
домножається на основу системи числення в степені, задаваємій порядком.
Наприклад, число 200 записується у вигляді 0,2×103, а
число 0,000312 = 0,312×10-3. Відповідно записуються і двійкові числа. Mантиса і
порядок зображаються в двійковому коді, а основою є двійка. Наприклад, число
0,111×210
= 11.10 в десятковій системі зображається як 0,875×22 = 3,5. В
строчці пам’яті такі числа зберігаються у вигляді двох груп цифр: перша
група, мантиса, визначає саме число, друга - порядок, - місце коми
в числі (рис.1.14).
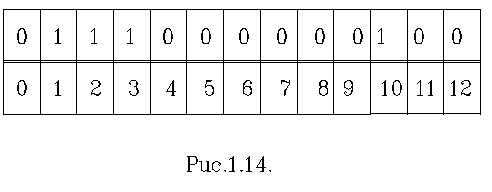 В нульовому
елементі строчки пам’яті зобра-жається знак числа (для
приведеного вище двій-кового числа, що запи-сане в строчку пам’яті - “0”). Далі задаються вісім розрядів самого числа.
(стовбці 1-8). Якщо воно задається меншою кількістю розрядів,
то вільні елементи пам’яті справа від числа заповнюються
нулями. В дев’ятому розряді зображається знак порядку, а в решті, по аналогії з мантисою,
число, що визначає порядок.
В нульовому
елементі строчки пам’яті зобра-жається знак числа (для
приведеного вище двій-кового числа, що запи-сане в строчку пам’яті - “0”). Далі задаються вісім розрядів самого числа.
(стовбці 1-8). Якщо воно задається меншою кількістю розрядів,
то вільні елементи пам’яті справа від числа заповнюються
нулями. В дев’ятому розряді зображається знак порядку, а в решті, по аналогії з мантисою,
число, що визначає порядок.
При використанні такої форми запису величина числа порядка задається так, щоб перша значаща цифра мантиси не дорівнювала “0”. Така форма запису називається нормальною [….].
Мінімальне позитивне число, що може бути записане при нормальній формі в строчці пам’яті визначається мінімальною мантисою 0,1000..02 та максимальним негативним порядком 111..12 .При кількості k розрядів порядка, мінімальне десяткове число, що може бути записаним, визначається формулою:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.