Метод, оснований на використанні карт Карно характеризується своєю простотою і наглядністю
Для пояснення методу перш за все сформулюємо основні властивості карт Карно:
·
 клітки карти, координати яких відрізняються
лише параметрами одної зміної називаються сусідніми;
клітки карти, координати яких відрізняються
лише параметрами одної зміної називаються сусідніми;
· сусідні клітки, значення функцій в яких являється або тільки істиним, або тільки хибним можуть обєднуватись в групи по 2m кліток, де m- ціле число (m=0,1,2,3…);
· при переході до аналітичної форми запису логічної функції з карти вона може записуватись незмінними координатами обєднаних груп кліток;
· в випадку неповністю визначеної функції невизначені клітини можуть бути довизначеними, виходячи з умови одержання більшої кількості об’єднаних кліток.
· одна клітка може об’єднуватись в декілька груп.
Реально використання карт Карно для мінімізації логічних функцій базується на наглідному використанні операції склеювання. Дійсно, дві сусідні клітки відрізняються лише одною змінною. Тому, об’єднуючи їх, ми фактично записуємо лише незмінні координати, тобто, виносимо їх за дужки. В дужках залишаються змінюємі координати, які об’єднуються в 1 операвцією склеювання.
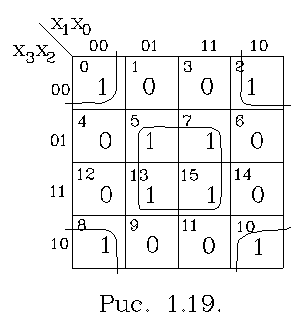
Як приклад мінімізації розглянемо функцію що представлена на рис.1.19.
Об’єднуючи сусідні клітки з істиними значеннями функції (клітки 0,2,8,10 та клітки 5,7,13,15) записуємо їх незмінні координати:
Мінімізована логічна функція має вигляд:
Аналогічний результат буде одержаний і при об’єднанні кліток з нулями.
Для вертикальної групи кліток (клітки 1,3,9,11) находимо:
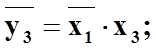 |
Мінімізована функція:
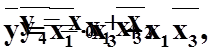 |
 Мінімізація
неповністю визначених логічних функцій. Серед логічних
функцій зустрічаються такі, досконалі форми яких містять невизначені мінтерми
(макстерми). З точи зору інженерної практики це означає що розробляєма
аппаратура повинна бути байдужою до відповідних комбінацій логічних змінних.
Зустрічаються і інші ситуації, при яких в деяких комбінація змінних має місце
неоднозначність логічної функції. В обох випадках наявність неоднозначності
використовується з метою забезпечення мінімальної форми логічної функції.
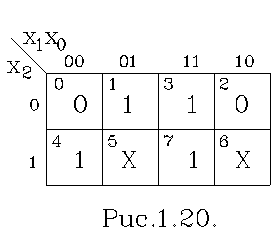
Розглянемо приклад логічної функції, що приведена на рис. 1.20. Невизначеність
значень логічної функції, що відображена в клітках 5,6 може бути вико-ристана
для мінімізації. Підстановка в указані клітки значень, відповідних “1”,дає
можливість об’єднати групи кліток 1,3,5,7, і 4,5,6,7 і одержати слідуючу
мінімізовану функцію
Мінімізація
неповністю визначених логічних функцій. Серед логічних
функцій зустрічаються такі, досконалі форми яких містять невизначені мінтерми
(макстерми). З точи зору інженерної практики це означає що розробляєма
аппаратура повинна бути байдужою до відповідних комбінацій логічних змінних.
Зустрічаються і інші ситуації, при яких в деяких комбінація змінних має місце
неоднозначність логічної функції. В обох випадках наявність неоднозначності
використовується з метою забезпечення мінімальної форми логічної функції.
Розглянемо приклад логічної функції, що приведена на рис. 1.20. Невизначеність
значень логічної функції, що відображена в клітках 5,6 може бути вико-ристана
для мінімізації. Підстановка в указані клітки значень, відповідних “1”,дає
можливість об’єднати групи кліток 1,3,5,7, і 4,5,6,7 і одержати слідуючу
мінімізовану функцію
Недовизначені функції часто зустрічаються при реалізації перетворювачів кодів.
З допомогою карт Карно легко вирішуються задачі мінімізації функцій з кількістю змінних до 6 включно.
Сумісна мінімізація декількох логічних функцій. В практичних задачах цифрової електроніки дуже часто зустрічаються ситуації, коли використовується декілька різних функцій з однаковими змінними. Як приклад, розглянемо слідуючі дві функції:
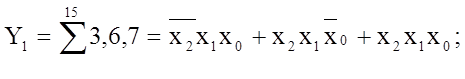
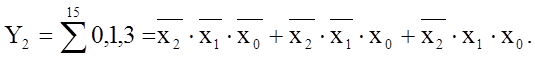
Кожну з них можна мінімізувати окремою При такій мінімізації маємо:
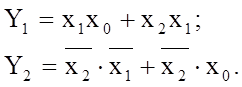
Обидві функцій можуть реалізовуватись окремо.
Але порівнюючи приведені функції, бачимо, що в обох з них є загальний мінтерм. Це дає підставу окремо реалізувати загальний мінтерм, а решту мінімізовувати незалежно для кожної з функцій. В такому випадку маємо:
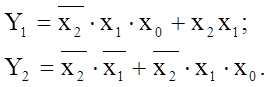
В такому випадку при побудові схеми окремо реалізуються всі терми, а потім виконується їх об’єднання через функцію АБО.
Мінімізація логічних функцій з великою кількістю змінних
Практичні комбінаційні схеми можуть мати десятки- сотні входів і виходів і описуватись сотнями-тисячами термів. В таких випадках для мінімізації, як кажуть, вручну, широко використовується метод декомпозиції. Він полягає в слідуючому. Логічна функція з великою кількістю змінних, наприклад
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.