Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 6

         ( a_-2× P^-1 ….+ a_-k×P^-k+1 + .. )×Р

Цей процес продовжується до тих пір, поки дробна частина результату перемноження лівої частини не стане рівною нулю, або поки не буде виділений період повторяємості цифр.

Приклад: Перевести число А = 0.375₁₀ в двійкову систему счислення .

0.375 × 2 = 0.75;             0- перша цифра результату.

0.75   × 2 = 1.5;               1- друга цифра результату.

0.5     × 2 = 1                   1- остання цифра результату.

Внаслідок виконання перетворень отримали результат

   0.375₁₀ = 0.011₂

Приклад: привести число А =0.109375₁₀ в шістнадцятирічну систему счислення

0.109375× 16 = 1.75           1- перша цифра результату.

0.75 × 16        = 12.0            12=С- остання цифра результату.

В результаті отримана відповідь: 0.109375₁₀ = 0.1С₁₆.

Переводити числа з одної недесятичної системи счислення в аналогічну іншу виконується шляхом послідовного перетворення Р-ічної системи счислення в десятичну, а потім виконується друга частина операції. Виключення складає лише перевід з двійкової системи счислення в шістнадцятирічну і навпаки.        

       1.3. Коди та їх характеристика.

        1.3.1. Коди з паралельною формою представлення інформації

        В попередньому параграфі було розглянуто перетворення аналогового сигналу в послідовність сигналів,  які умовно приймають лише значення  “1” та “0”.  Система счислення,  в якій використовуються лише два знаки для відображення інформації називається двійковою,  основою якої є число 2.  По аналогією з десятковою,  двійкова  система счислення є позиційною і будь-яке десяткове число може бути представлене двійковим рядом,  що вміщює лише “1” та “0”. В відповідності з алгоритмом:

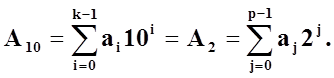
                                      (1.14)

де =0. . 9 -цифри і-того розряду десяткового числа; =0. 1 - відповідно цифри  j-того розряду десяткового числа.  Розряди чисел рахуються зліва направо. Дробні  числа  представляються  доповненням суми  (1.14)   від’ємними  степенями  числа  2.

Електронні системи,  що оперують сигналами, які відповідають лише рівням “1” та “0” називаються цифровими.  Так же і відповідні сигнали.

         Як в теорії інформації, так і в  практиці цифрової схемотехніки вико-ристовується багато різноманітних кодів.  Визначимось з основною термінологією.  

          Код,  відповідно  до [17]. - це універсальний спосіб відображення інформації при її зберіганні,  передачі і обробці в вигляді системи однозначних відповідностей між елементами повідомлень і сигналами,  з допомогою яких ці елементи можна зафіксувати.  Іншими словами,  кодування - це однозначне перетворення символів одного алфавіту в символи іншого,  а код - правило,  закон,  алгоритм,  при якому відбувається це перетворення.  Комбінації символів,  що належать до данного коду,  називаються кодовими словами.  Символи,  з допомогою яких повідомлення трансформується в код,  являються вторинним алфавітом.  Процес відновлення вмісту повідомлення по відомому коду називається декодуванням.  Необхідною умовою декодування є взаємнооднозначна відповідність кодових слів в вторинному алфавіті кодуємим символам первинного алфавіту.  При передачі кодових символів по лініях зв’язку вони повинні бути розділені так,  щоб кожен символ міг бути прийнятим самостійно,  що виконується з використанням різних принципів їх розділення.  Розділення символів може бути просторовим,  часовим  і якісним.  Просторове розділення по суті є багатоканальним зв’язком і при його використанні відпадає необхідність в спеціальних методах кодування.  При якісному розділенні між символами повинно бути як мінімум дві розділюючи ознаки,  наприклад,  тривалість імпульса,  паузи,  які легко відрізняються на приймальній стороні лінії зв’язку.  Якісне розділення дає можливість одночасної передачі інформації від різних об’єктів по одному каналу зв’язку.  Прикладом якісного розділення є частотне розділення (мо-ногармонічний  сигнал  при  імпульсі  має одну частоту,  а при паузі – іншу).